高一数学第一学期期中考试
高一数学试题
第Ⅰ卷
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设A，B，C为非空集合，M=A∩C，N=B∩C，P=M∪N则必有 （ ）
A．C∩P=C B．C∩P=P C．C∩P=C∪P D．C∩P=
2．不等式2x+5≤7的解集是 （ ）
A．
B．
C．
D．
3．若
（ ）
A．1 B．3 C．15 D．30
4．设非空集合A、B、C，若“a∈A”的充要条件是“a∈B且a∈C”，那么“a∈B”是“a∈A”的 （ ）
A．充要条件 B．必要不充分条件
C．充分不必要条件 D．既不充分也不必要条件
5．函数
的定义域是 （ ）
A．
B．
C．
D．
6．函数
的值域是 （ ）
A．[0，1] B．[0，2] C．[－1，1] D．[1，2]
7．设
为偶函数且
上是增函数，则
的大小顺序是 （ ）
A．
B．
C．
D．
8．若
为常数）的反函数是
，则a、b、c的值是（ ）
A．a=3，b=2，c=1 B．a=－3，b=1，c=2
C．a=1，b=2，c=－3 D．a=1，b=－3，c=2
9．已知不等式
恒成立，则实数a的取值范围是 （ ）
A．
B．a>2 C．a>1 D．
|
的解集为 （ ）
A．
B．
C．
D．
11．设函数
的图象关于直线y=x对称，则
= （ ）
A．
B．－1 C．
D．0
12．已知函数
，构造函数
时，
，当
（ ）
A．有最小值0，无最大值 B．有最小值－1，无最大值
C．有最大值1，无最小值 D．无最小值，也无最大值
二、填空题：本大题共4小题，每小题4分，共16分。答案填在题中横线上。
13．已知点（x，y）在映射f下的象是（
），则点（1，2）的原象是
14．函数
的单调增区间是
15．
的定义域为[0，1]，则
的定义域为
16．若
的两个根，则
的最大值是
三、解答题：本大题共6小题，共74分。解答应实际情况出文字说明，证明过程或演算步骤。
|
设
的值。
18．（本小题满分12分）
已知命题p：函数
的反函数，实数m满足不等式
，命题q：实数m使方程
有实根，若命题p、q中有且只有一个真命题，求实数m的范围。
19．（本题满分12分）
若函数
互为反函数，求a、b、c的值。
20．（本小题满分12分）
已知函数
（1）写出函数的单调增区间，并用定义加以证明：
（2）设函数
试利用（1）的结论直接写出该函数的值域（用区间表示）。
21．（本小题满分12分）
有甲、乙两种商品，经营销售这两种商品所能获得的利润，依次是P和Q（万元），
它们与投入的资金x（万元）的关系有公式，
，今有3万元资金投
入经营甲乙两种商品，设投入乙的资金为x（万元），获得的总利润y（万元）。
（1）用x表示y；
（2）x为何值时，y有最大值，并求出这个最大值。
22．（本小题满分14分）
已知函数
，对于定义域内任意x、y恒有
恒成立。
（1）求
；
（2）证明方程
有且仅有一个实根；
（3）若
恒成立，求实数a的取值范围。
河北省邯郸一中2007—2008学年度高一第一学期期中考试
数学试题参考答案
一、选择题：
BDCBD DACDA AB
|
13．
14．
15．
16．18
三、解答题：
17．解：由
∵A={a} ∴方程
有两个相等实根为a，
∴将a代入方程得：
①
又由△=0得 
② 解得 
18．解：由
又
∴p：－5<m
因为方程
∴q：m<0
若命题p、q中有且只有一个真命题，存在两种情况：
（1）当p为真命题，q为假命题时，
（2）当q为真命题，p为假命题时，
综上当命题p、q中有且只有一个真命题时，
，或
0
19．解：∵
∵
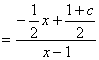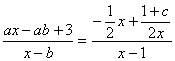恒成立，
比较对应项得 －b=－1，
即
20．解：（1）的单调增区间为
下面用定义证明：设
是上任意两个值且 
∵
∴
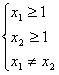又
∴
∴
上是增函数。
（2）的最大值
，值域为[3，6]
21．解：（1）
（2）令
，则
当t=
答：当
万元时，总利润最大为
万元。
22．解：（1）令x=y=1， ∴
，∴
；
（2）任取
，则
又定义域内任意x、y恒有 
∴
∴函数在其定义域内为增函数，由（1）和，所以1为方程的一个实根，若还存在一个
，因为函数在其定义域内为增函数，必有
，故方程有且仅有一个实根；
（3）由（2）知函数在其定义域内为增函数
当
恒成立
即
时恒成立
∵