高一数学必修4模块测试卷与参考解答
一.选择题：
1．－215°是 （ B ）
（A）第一象限角 （B）第二象限角
（C）第三象限角 （D）第四象限角
考查象限角概念，简单题。
2．角
的终边过点P（4，－3），则
的值为 （ C ）
（A）4 （B）－3 （C）
（D）
考查三角函数定义，简单题。
3．若
，则角
的终边在 （ C ）
（A）第二象限 （B）第四象限 （C）第二、四象限 （D）第三、四象限
考查三角函数符号，简单题。
4．函数
的最小正周期是 （ A ）
（A）
（B）
（C）
（D）
考查三角恒等变换，三角函数的周期，中等题。
5．给出下面四个命题：①
；②
；③
；
④
。其中正确的个数为 （ B ）
（A）1个 （B）2个 （C）3个 （D）4个
考查向量的运算，简单题。
6．向量
，
，则
（ B ）
（A）
∥
（B）⊥
（C）与的夹角为60° （D）与的夹角为30°
考查向量的坐标运算及向量的夹角，简单题。
7. 在下面给出的四个函数中，既是区间
上的增函数，又是以为周期的偶函数的是( D )
（A）
（B）
（C）
（D）
考查三角函数的性质，简单题。
8.若=(2,1)，=(3,4)，则向量在向量方向上的投影为（ B ）
（A）
（B）2 （C）
（D）10、
考查向量的投影，简单题。
9．化简
的结果是 （ D ）
（A）
（B）
（C）
（D）
考查倍角公式，中等题。
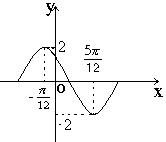
10．函数
在一个周期内的图象如下，此函数的解析式为（ A ）
（A）
（B）
（C）
（D）
11．在锐角△ABC中，设
则x,y的大小关系为（ B
）
（A）
（B）
（C）
（D）
考查两角和的余弦公式，中等题。
12．若
，则
的值是 （ D ）
（A）-2 （B）-1 （C）1 （D）2
考查三角变形，中等题。
二.填空题：（每小题4分，共20分。请将答案直接填在题后的横线上。）
13．已知点A（2，－4），B（－6,2），则AB的中点M的坐标为 （－2，－1） ；
考查中点坐标公式，简单题。
14．若
与
共线，则
＝ －6 ；
考查共线向量，简单题。
15．若
，则
= －3 ；
考查同角三角函数的基本关系，简单题。
16．函数
的值域是
[－1,3]
；
考查三角函数的值域，简单题。
17．已知
，与的夹角为
，那么
=
。
考查向量模的运算，中等题。
三．解答题（本大题共5题，共.44分，解答题应写出文字说明、演算步骤或证明过程.）
18．（本小题共8分，每题4分）求值：
（1）
； （2）
解：（1）
……（4分）
考查诱导公式，特殊角的三角函数值，简单题。
（2）原式=
=
……（8分）
考查和角公式的运用及特殊角的三角函数值，简单题。
19．（本小题8分）已知3sin
＋cos
＝２．（cosＡcosＢ≠0）
求tanＡtanB的值．
解：由已知有：３·
＋
＝２
……（3分）
∴－３cos(A＋B)+cos(A－B)＝0,
∴－３(cosAcosB－sinAsinB)+(cosAcosB＋sinAsinB)＝0, ………（6分）
∴cosAcosB＝2sinAsinB, ∴tanＡtanB=
…………（8分）
20．（本小题8分）设
，
，
，
∥
，试求满足
的
的坐标（O为坐标原点）。
解：设
，由题意得：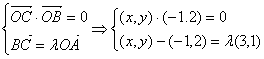
……（3分）
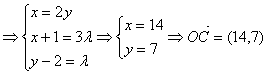……（6分）
……（8分）
考查向量的平行与垂直、向量的坐标运算，简单题。
21，（本小题10分）已知函数
。
（Ⅰ）求
的周期和振幅；
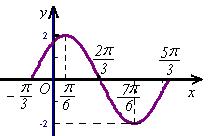
（Ⅱ）在给出的方格纸上用五点作图法作出在一个周期内的图象。
（Ⅲ）写出函数的递减区间。
解：（Ⅰ）
＝
＝
……（2分）
函数的周期为T＝
，振幅为2。
……（.4分）
（Ⅱ）列表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | 2 | 0 | -2 | 0 |
……（6分）
图象如上（作图不规范者扣1分）。 ……（8分）
（Ⅲ）由
解得：
所以函数的递减区间为
……（10分）
考查两角和与差的三角函数及函数
的图象及性质。中等题。
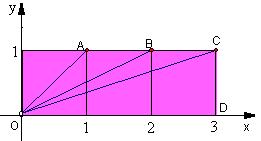22．（本小题10分）如图，三个同样大小的正方形并排一行。
（Ⅰ）求与
夹角的余弦值；
（Ⅱ）求∠BOD＋∠COD；
解：（Ⅰ）因为A（1,1），B（2,1）
所以＝（1,1），＝（2,1）……（2分）
cos∠AOB＝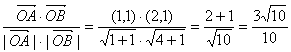
. ……（4分）
（Ⅱ）因为C（3,1），D（3，0），所以tan∠BOD＝，tan∠COD＝
……（6分）
所以 tan(∠BOD＋∠COD)=
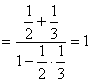……（8分）
又因为∠BOD和∠COD均为锐角，故∠BOD＋∠COD＝45° ……（10分）
考查向量数量积的几何意义，向量夹角求法，两角和的正切，。中等题。