高一数学模块一第二章单元测试试题
说明:本试题测试时间为50分钟,满分100分
一、选择题:(本大题共8小题,每小题6分,共48分)答案填在答题卷答题卡内,否则不计分.
1、 函数
（
>0且≠1）的图象必经过点 （ ）
（A）（0,1） （B） (1,1) （C） (2,3) （D）(2,4)
2、三个数
之间的大小关系是（ ）
（A）
. （B） 
（C）
（D）
3、函数 的定义域为 （ ）
（A）[1，3] （B）
（C）（1，3） （D）（1，2）∪（2，3）
4、已知镭经过100年，剩留原来质量的95．76%，设质量为1的镭经过x年的剩留量为y，则y与x的函数关系是（ ）
（A）y=(0．9576)
（B）y=(0．9576)100x（C）y=( )x （D）y=1－（0．0424）
5、函数y=
在[1,3]上的最大值与最小值的和为1，则a =（
）
（A） （B） 2 （C） 3 （D）
6、下列函数中，在区间（0，2）上不是增函数的是（ ）
（A） 
（B）
（C） 
（D）
7、函数 与
（
）在同一坐标系中的图像只可能是（ ）
；
； 
； 
。
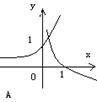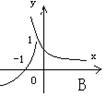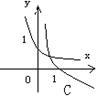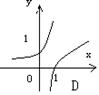8、（4～10班做）对于函数f(x)定义域中任意的x1，x2（x1≠x2），有如下结论：
①f (x1+x2)=f (x1)+f (x2)；② f (x1·x2)=f (x1)+f (x2 ) ；③
>0；
④
.当f(x)=log2 x时，上述结论中正确结论的序号选项是
（A） ①④ （B） ②④ （C）②③ （D）①③
8、（1～3班做）已知
是
上的减函数，那么的取值范围是
（A）
（B）
（C）
（D）
二、填空题(本大题共4小题,每小题5分,共20分)
9、 函数
的定义域是
．
10、求值：
＝________ _．
11、已知幂函数
的图象经过点(3,
)，那么这个幂函数的解析式为 .
12、设
则
__________
三、解答题(第12题7分，13题10分，第14题15分，共32分, 解答应写出文字说明，证明过程或演算步骤)
13、求log2．56．25+lg
+ln
+
的值．
14、已知m>1，试比较（lgm）0．9与（lgm）0．8的大小．
15、已知
（Ⅰ）证明函数f ( x )的图象关于
轴对称；（4分 ）
（Ⅱ）判断
在
上的单调性，并用定义加以证明；（7分）
（4～10班做）（Ⅲ）当x∈［1，2］时函数f (x )的最大值为
，求此时a的值. （4分）
（1～3班做）（Ⅲ）当x∈［－2，－1］时函数f (x )的最大值为，求此时a的值. （4分）
高一数学模块一第二章单元测试答题卷
班级 座号 姓名 得分
一、选择题答题卡(本大题共8小题,每小题6分,共48分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
|
|
二、填空题(本大题共4小题,每小题5分,共20分)
9、 ；10、 ；11、 ；12、 .
三、解答题 (第12题7分，13题10分、14题15分，共32分, 解答应写出文字说明，证明过程或演算步骤)
13、
14、
15、
高一数学模块一第二章单元测试参考答案
一、选择题 DBDA CCAC
7、取a=2和a = 作图筛选得A
8、解：依题意，有0<a<1且3a－1<0，解得0<a<
，又当x<1时，（3a－1）x＋4a>7a－1，当x≥1时，logax≤0，所以7a－1³0解得a³
故选C
二、填空题
8、
；9、 4 ；10、
；11、 .
11、设这个幂函数的解析式为 ，将(3, )代入得
12、.【解析】
.
三、解答题 (本大题有3小题,共32分) 解答应写出文字说明，证明过程或演算步骤)
12、解： 原式＝2－2＋ ln
＋
…………3分
＝ ＋6 …………5分
＝
…………7分
14、解：∵m>1，∴lgm＞0；以下分类为①lgm＞1，②lgm=1；③0＜lgm＜1
三种情形讨论（lgm）0．9与（lgm）0．8的大小．…………2分
①当lgm＞1即m＞10时，（lgm）0．9＞（lgm）0．8；…………5分
②当lgm=1即m=10时，（lgm）0．9=（lgm）0．8；…………7分
③当0＜lgm＜1即1＜m＜10时，（lgm）0．9＜（lgm）0．8．…………10分
15、解：（Ⅰ）要证明函数f ( x )的图象关于轴对称则只须证明函数f ( x )是偶函数…1分
∵x∈R …………2分
由
…………3分
∴函数f ( x )是偶函数，即函数f ( x )的图象关于轴对称…………4分
（Ⅱ）证明：设
，则
=
（1）当a>1时，
由0<
，则x1+x2>0，则
、
、
、
；
<0即
；
（2）当0<a<1时，
由0<，则x1+x2>0，则、、
、
；
<0即；
所以，对于任意a（
），f(x)在上都为增函数．
（4～10班做）（Ⅲ）由（Ⅱ）知f(x)在上为增函数，则当x∈［1，2］时，函数f (x )亦为增函数；
由于函数f(x)的最大值为，则f(2)=
即
，解得
，或
（1～3班做）（Ⅲ）由（Ⅰ）（Ⅱ）证知f(x) 是偶函数且在上为增函数，则知f(x)在
上为减函数；
则当x∈［－2，－1］时，函数f (x )为减函数
由于函数f(x)的最大值为，则f(－2)=
即
，解得，或