高一数学必修二测试试题
班级： 姓名： 命题:刘建军
一、选择题：(本大题共12小题，每小题5分，共60分)
1．若直线的倾斜角为1200，则直线的斜率为：
A．
B．－
C．
D．
2．下列命题中，错误的是：
A．平行于同一条直线的两个平面平行.
B．平行于同一个平面的两个平面平行.
C．一个平面与两个平行平面相交，交线平行.
D．一条直线与两个平行平面中的一个相交，则必与另一个平面相交.
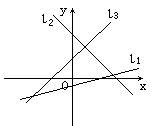3．若图中直线
的斜率分别为k1,k2,k3,则
A.k2<k1<k3 B.k3<k2<k1
C.k2<k3<k1 D.k1<k3<k2
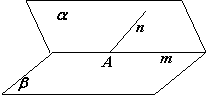4．如图所示，用符号语言可表达为
A．α∩β＝m，n
α，m∩n＝A
B．α∩β＝m，n∈α，m∩n＝A
C．α∩β＝m，nα，Am，A n
D．α∩β＝m，n∈α，A∈m，A∈ n
5．给出下列四个命题：
① 若两条直线和第三条直线所成的角相等，则这两条直线互相平行.
② 若两条直线都与第三条直线垂直，则这两条直线互相平行.
③ 若两条直线都与第三条直线平行，则这条直线互相平行.
④ 若两条直线都与同一平面平行，则这条直线互相平行.
其中正确的命题的个数是：
A．1个 B．2个 C．3个 D．4个
6．在正方体ABCD-A1B1C1D1中，与BD1所成的角为900的表面的对角线有
A．4条 B．5条 C．6条 D．8条
7．下列直线中，斜率为
，且不经过第一象限的是
A．3x＋4y＋7=0 B．4x＋3y＋7=0
C．4x＋3y-42=0 D．3x＋4y-42=0
8．已知两直线
与
平行，则
等于
A． 
B．
C．
D．
9．下列命题中正确的是（其中a、b、c为不相重合的直线，
为平面）
①若b∥a，c∥a，则b∥c ②若b⊥a，c⊥a，则b∥c
③若a∥，b∥，则a∥b ④若a⊥，b⊥，则a∥b
A．①、②、③、④ B．①，④
C．① D．④
10．已知三棱锥
的棱长都相等，
分别是棱
的中点，则
所成的角是：
A．
B．
C．
D．
11．过点(1,2),且在两坐标轴上的截距相等的直线有
A. 1条 B. 2条 C. 3条 D. 4条
12．设
为两两不重合的平面，
为两两不重合的直线，给出下列四个命题：
①若
，
，则
；②若
，
，
，
，则；③若，
，则
； ④若
，
，
，
，则
。其中真命题的个数是
A．1 B．2 C．3 D．4
一、选择题：(本大题共12小题，每小题5分，共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题：(本大题共5小题，每小题4分，共20分)
13．过点（－1，2）且倾斜角为450的直线方程是____________
14．已知直线
和平面，且
则
与的位置关系是
.
15．直线 y = 2x 关于 x 轴对称的直线方程是_______________.
16．如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线必在第一个平面内．用数学符号语言可叙述为：______________________________.
17．已知为不垂直的异面直线，是一个平面，则在上的射影有可能是：
① 两条平行直线；②两条互相垂直的直线；③同一条直线；④一条直线及其外一点
在上面的结论中，正确结论的编号是 （写出所有正确结论的编号）
三、计算题：(本大题4小题，共40分)
18．(本小题满分12分)
求过点
，且在两坐标轴上的截距互为相反数的直线
的方程
19．(本小题满分14分)
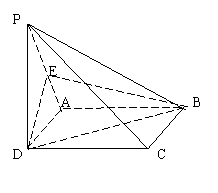
如图：已知四棱锥
中，
是正方形，E是
的中点，求证：(1)
平面
(2)平面PBC⊥平面PCD
 |
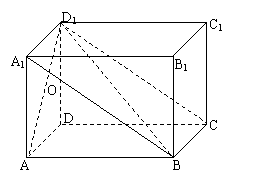20．(本小题满分14分)
在长方体ABCD-A1B1C1D1中，AB=
，
B1B=BC=1，
（1）求D D1与平面ABD1所成角的大小；
（2）求面B D1C与面A D1D所成二面角的大小；
高一数学必修二单元测试答案
一、选择题：(本大题共12小题，每小题5分，共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | A | A | A | A | C | B | C | B | B | B | B |
二、填空题：(本大题共5小题，每小题4分，共20分)
13．
x-y+3=0
14．
∥
15．y=－2x
16． 
17．① ② ④
第18题解答：
解：设所求直线的方程为x-y+m=0或y=kx
6分
把点 代入上述方程得：m=-3或k=
10分
故 所求直线的方程为x-y-3=0或2x-5y=0
12分
第19题解答：
解：（1）连接AC交BD与O,连接EO, ∵E、O分别为PA、AC的中点
∴EO∥PC ∵PC
平面EBD,EO
平面EBD ∴PC∥平面EBD 7分
（2）∵PA^平面ABCD, PA平面ACD，∴平面PCD^平面ABCD，
∵ABCD为正方形 ∴ BC^CD，∵平面PCD∩平面ABCD, BC平面ABCD
∴∴BC^平面PAB
又∵ BC平面PBC，∴平面PBC^平面PCD．
14分
第20题解答：
解：（1）连接A1D交AD1于O，∵ABCD-A1B1C1D1为长方体，而B1B=BC，则四边形A1ADD1为正方形，∴A1D^AD1，
又∵AB^面A1ADD1，A1D面A1ADD1，∴AB^A1D，∴A1D^面ABD1，
∴ÐDD1O是D D1与平面ABD1所成角， 5分
∵四边形A1ADD1为正方形，∴ÐDD1O=450，则D D1与平面ABD1所成角为450．7分
（2）连接A1B，∵A1A^面D1DCC1，D1D、DC面D1DCC1，∴A1A^ D1D、A1A^DC，
∴ÐDD1C是面B D1C与面A D1D所成二面角的平面角，
12分
在直角三角形D1DC中，∵DC=AB=，D1D=B1B =1，∴ÐDD1C=600，
即面B D1C与面A D1D所成的二面角为600．
14分