高一数学必修模块Ⅰ终结性测试卷
试卷说明:本卷满分100分,考试时间90分钟。除规定不准用计算器的题目以外的题,若有需要,可用计算器。选择题只有一个正确答案,请将正确答案填涂在答题卡上。解答题写出必要的推演步骤。开放题说理有据,所举事实真实,与生活阅历贴近更好。交卷时只交答题卡和第二卷。
第Ⅰ卷
一、选择题。(共8小题,每题4分)
1、设集合A={x![]() Qx>-1},则
Qx>-1},则
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
![]()
![]()
2、设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B=
A、{1,2} B、{1,5} C、{2,5} D、{1,2,5}
3、函数![]() 的定义域为
的定义域为
A、[1,2)∪(2,+∞) B、(1,+∞) C、[1,2) D、[1,+∞)
4、设集合M={x-2≤x≤2},N={y0≤y≤2},给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是
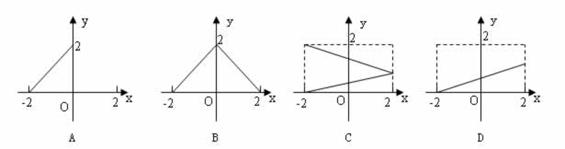
5、若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为
A、1.2 B、1.3 C、1.4 D、1.5
6、函数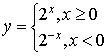 的图像为
的图像为
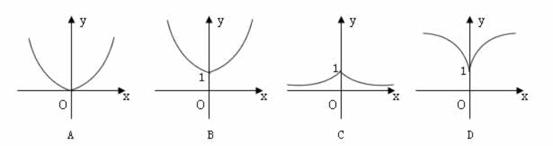
7、设![]() (a>0,a≠1),对于任意的正实数x,y,都有
(a>0,a≠1),对于任意的正实数x,y,都有
A、f(xy)=f(x)f(y) B、f(xy)=f(x)+f(y)
C、f(x+y)=f(x)f(y) D、f(x+y)=f(x)+f(y)
8、函数y=ax2+bx+3在(-∞,-1]上是增函数,在[-1,+∞)上是减函数,则
A、b>0且a<0 B、b=2a<0 C、b=2a>0 D、a,b的符号不定
第Ⅱ卷
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 13 | 14 | 15 | 16 | 17 | 18 | ||||
| 得分 | |||||||||
二、填空题(共4题,每题5分)
9、f(x)的图像如下图,则f(x)的值域为 ;
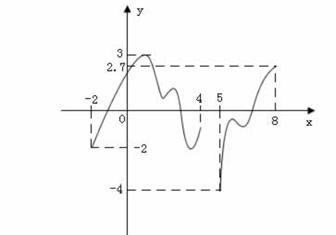
10、假设1995年我国的国民生产总值为a亿元,如每年平均增长8.2%,那么大约经过 年(精确到1)国民生产总值是1995年的2倍;
11、函数![]() 的反函数为
;
的反函数为
;
12、老师给出一个函数,请三位同学各说出了这个函数的一条性质:①此函数为偶函数;②定义域为![]() ;③在
;③在![]() 上为增函数.
上为增函数.
老师评价说其中有一个同学的结论错误,另两位同学的结论正确。请你写出一个(或几个)这样的函数
三、解答题(共48分,解答题写出必要的文字说明、推演步骤。)
13、(本题6分)设全集为R,![]() ,
,![]() ,求
,求![]() 及
及![]()
14、(本题8分)不用计算器求下列各式的值
⑴ 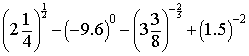 ⑵
⑵ ![]()
15、(本题8分)若函数f(x)=logax (a>0且a≠1)在[2,8]上最大值与最小值之差为2,求a的值
16、(本题8分)两份资料提供了两条看起来似乎矛盾的信息:
a)美国的农场从1982年的平均每农场428英亩逐年上升到1987年的平均每农场461英亩,似乎说明农业生产规模的扩大(下图1)
b)美国的农场数从1982年的240.1万个减少为1987年的217.3万个,似乎说明农业生产规模的缩小(下图2)
请根据这些信息作出判断,农业生产规模究竟是扩大了,还是缩小了?
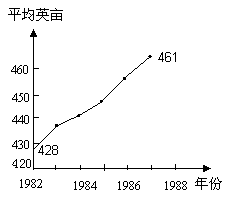

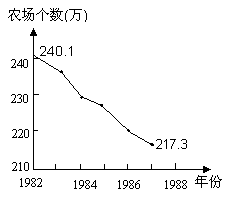

图1 图2
17、(本题10分)如图是一次舞会的盈利额P同售票数![]() 之间的关系图(其中保险部门规定:人数超过150的时候,须缴纳一定的公安保险等费用),请求出它的函数表达式,并写一段文字对图象从不同角度(如成本,赚钱,赔本等方面)加以解释
之间的关系图(其中保险部门规定:人数超过150的时候,须缴纳一定的公安保险等费用),请求出它的函数表达式,并写一段文字对图象从不同角度(如成本,赚钱,赔本等方面)加以解释
 |
18、(本题8分)某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件,为了估测以后各月的产量,以这三个月产品数为依据,用一个函数模拟此产品的月产量y(万件)与月份数x的关系,模拟函数可以选取二次函数y=px2+qx+r或函数y=abx+c(其中p、q、r、a、b、c均为常数),已知4月份该新产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?求出此函数。
高一数学必修模块Ⅰ终结性测试题参考答案及评分标准
一、 选择题(4×8)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | D | A | C | C | B | B | B |
二、 填空题(共4题,每题5分)
9、[-4,3]
10、9
11、![]()
12、![]() 或
或![]() 或
或![]()
第12题评分说明:或答对一个给4分,答对两个不同类型的函数奖励1分(即给5分),答对三个不同类型的函数奖励2分(即给6分)。
三、 解答题(共48分)
13. 解:![]() ………………………3’
………………………3’
![]() ……………6’
……………6’
14.
解(1)原式=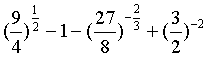
=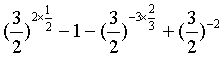
=![]()
=![]() ……………………4’
……………………4’
(2)原式=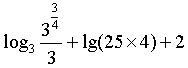
=![]()
=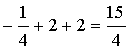 ……………………3’
……………………3’
15. 解:(1)当0<a<1时,由![]() 在
在![]() 上是减函
上是减函
数,得 ![]() ,
,![]() ……2’
……2’
由已知:![]() ……4’
……4’
(2)当a>1时
![]() ……6’
……6’
![]()
综上所述 ![]() ……………………8’
……………………8’
另解:当![]() ,
,![]() 是单调函数
是单调函数
![]() 下略
下略
参照以上标准评分
16. 解:从1982年到1987年,农场平均面积增加了33英亩,而农场个数减少了22.8万个。单独的每条信息都不能解释农业生产规模的扩大或缩小,但从农场总面积来看,1982年和1987年分别时:
![]() (万英亩)
(万英亩)
![]() (万英亩)
……………4’
(万英亩)
……………4’
共减少了![]() (万英亩),说明从1982年到1987年美国共流失了2587.5万英亩的农田,因此可说明农场规模是缩小了。
(万英亩),说明从1982年到1987年美国共流失了2587.5万英亩的农田,因此可说明农场规模是缩小了。
…………………8’
17. 解:由图像可求得函数解析式为
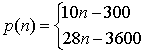
![]() ……………3’
……………3’
从不同角度剖析图像,下面提供几条参考性解释
(1)当售票数为0时,舞场正常开放,要支付水电、器材等成本费300元; ……………………4’
(2)当售票数n=30时,可达到不赔不赚,n<30时,则要赔本;
………………………5’
(3)当30<n![]() 时,利润与售票数呈直线上升,n=150时达到最大值1200元;
……………………6’
时,利润与售票数呈直线上升,n=150时达到最大值1200元;
……………………6’
(4)当150<n<172时,利润没有n=150人时多,即人数超过172时,利润超过1200元; ……………………7’
(5)当人数达到200人时,利润可达到最大值2000元。 ……8’
以上评分标准仅供参考,另有几点说明:
(1)若学生能从问题本身出发,从策略上描述本题所反映的实际现象,可酌情给分;
(2)学生对n=30,150,172,200几个点的认识,可视为反映不同思维水平和能力水平,评分应有所区分。
18. 解:若y=![]() 则由题设
则由题设
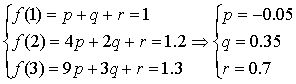 ………………2’
………………2’
![]() …………3’
…………3’
若![]() 则
则
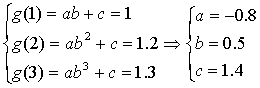 ………………5’
………………5’
![]() ………………7’
………………7’
![]() 选用函数
选用函数![]() 作为模拟函数较好
………………8’
作为模拟函数较好
………………8’