高一数学教学质量监测考试强化训练
说明：本试卷满分100分。另有附加题10分，附加题得分不计入总分。
一、 选择题（12×3分＝36分）(请将答案填在下面的答题框内)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、下列命题为真命题的是（ ）
A. 平行于同一平面的两条直线平行； B.与某一平面成等角的两条直线平行；
C. 垂直于同一平面的两条直线平行； D.垂直于同一直线的两条直线平行。
2、下列命题中错误的是：（ ）
A. 如果α⊥β，那么α内一定存在直线平行于平面β；
B. 如果α⊥β，那么α内所有直线都垂直于平面β；
C.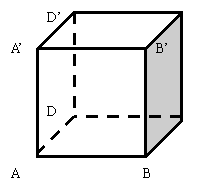 
如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；
D.
|
3、右图的正方体ABCD-A’B’C’D’
中,异面直线AA’与BC所成的角是（ ）
A. 300 B.450 C. 600 D. 900
|
4、右图的正方体ABCD- A’B’C’D’中，
二面角D’-AB-D的大小是（ ）
A. 300 B.450 C. 600 D. 900
5、直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则（ ）
A.a=2,b=5; B.a=2,b=
; C.a=
,b=5;
D.a=,b=.
6、直线2x-y=7与直线3x+2y-7=0的交点是（ ）
A (3,-1) B (-1,3) C (-3,-1) D (3,1)
7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是（ ）
A 4x+3y-13=0 B 4x-3y-19=0
C 3x-4y-16=0 D 3x+4y-8=0
8、正方体的全面积为a,它的顶点都在球面上，则这个球的表面积是：（ ）
A.
; B.
; C.
; D.
.
9、已知一个铜质的五棱柱的底面积为16cm2,高为4cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（ ）
A.
2cm; B.
;
C.4cm;
D.8cm。
10、圆x2+y2-4x-2y-5=0的圆心坐标是：（ ）
A.(-2,-1); B.(2,1); C.(2,-1); D.(1,-2).
11、直线3x+4y-13=0与圆
的位置关系是：（ ）
A. 相离; B. 相交; C. 相切; D. 无法判定.
12、圆C1: 
与圆C2:
的位置关系是（ ）
A、外离 B 相交 C 内切 D 外切
二、填空题（5×4=20）
13、底面直径和高都是4cm的圆柱的侧面积为 cm2。
14、两平行直线
的距离是
。
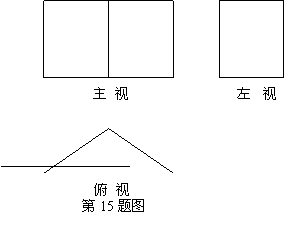
15、下图的三视图表示的几何体是
16、若直线
平行，则
。
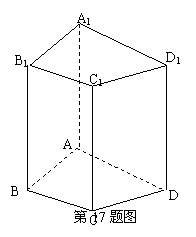
17、如图，在侧棱和底面垂直的四棱柱ABCD-A1B1C1D1中，当底面ABCD
满足条件
时，有
（写出你认为正确的一种
条件即可。）
 | |||
 | |||
三、解答题（共44分）
18、（6分）已知点A（-4，-5），B（6，-1），求以线段AB为直径的圆的方程。
19、（6分）已知三角形ABC的顶点坐标为A（-1，5）、B（-2，-1）、C（4，3），M是BC边上的中点。（1）求AB边所在的直线方程；（2）求中线AM的长。
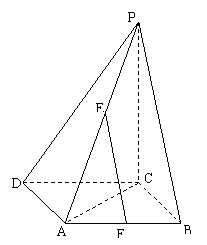20、（10分）如图，在边长为a的菱形ABCD中，
，E,F是PA和AB的中点。
（1）求证： EF平面PBC ;
（2）求E到平面PBC的距离。
21、（10分）已知关于x,y的方程C:
.
（1）当m为何值时，方程C表示圆。
（2）若圆C与直线l:x+2y-4=0相交于M,N两点，且MN=
,求m的值。
22、（12分）如图，在底面是直角梯形的四棱锥S-ABCD中，
(1)求四棱锥S-ABCD的体积;
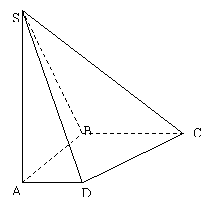(2)求证：
(3)求SC与底面ABCD所成角的正切值。
数学（必修4）参考答案
一、 选择题（12×3分＝36分）(请将答案填在下面的答题框内)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | B | B | A | A | B | C | B | C | D |
二、填空题（5×4=20）
13、
14、
15、三棱柱 16、
17、ABCD是菱形或是正方形或是对角线互相垂直的四边形
三、解答题（共32分）
18、解：所求圆的方程为：
………………2
由中点坐标公式得线段AB的中点坐标为C（1，-3）……4
……………………5
故所求圆的方程为：
………………6
19、解：（1）由两点式写方程得 
，……………………2
即 6x-y+11=0……………………………………………………3
或 直线AB的斜率为 
……………………………1
直线AB的方程为 
………………………………………2
即 6x-y+11=0…………………………………………………………………3
（2）设M的坐标为（
），则由中点坐标公式得
故M（1，1）………………………4
…………………………………………6
20、（1）证明：
…………………………………………1
又 
故 
………………………………………………4
（2）解：在面ABCD内作过F作
…………………………………5
……………………………………………7
又 
，
，
又，故点E到平面PBC的距离等于点F到平面PBC的距离FH。
…………………………………………………8
在直角三角形FBH中，
，
……………9
故点E到平面PBC的距离等于点F到平面PBC的距离，
等于
。………………………………………………………………10
21、解：（1）方程C可化为 
………………2
显然 
时方程C表示圆。………………4
（2）圆的方程化为
圆心 C（1，2），半径 
………………………………6
则圆心C（1，2）到直线l:x+2y-4=0的距离为
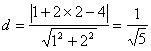………………………………………………8
，有 
得 
…………………………10
22、（1）解：
|
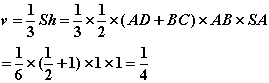
（2）证明：
|
又
|
|
（3）解：连结AC,则
就是SC与底面ABCD所成的角。
|
,
