高一数学学科第二学期期中考试试题
一、选择题（本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1、下列各图中表示的区域是不等式3x+2y+6≥0的解的是
 |
（ ）
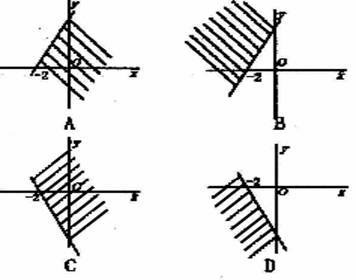2、等差数列
的前n项和为Sn，若a3+a17=10，则S19= （ ）
A．55 B．95 C．100 D．不能确定
3、已知是等比数列，an＞0，且a4a6+2a5a7+a6a8=36，则a5+a7等于 （ ）
A．6 B．12 C．18 D．24
4、下列不等式中解集为实数集R的是 （ ）
A．
B．
C．
D．
5、有分别满足下列条件的两个三角形：①
；②
，那么下列判断正确的是
( )
A．①②都只有一解 B．①②都有两解 C．①两解，②一解 D．①一解②两解
6、不等式
的解集是
（ ）
A．
B．
C．
D．
7、已知
，则
的最小值为
（ ）
A．8
B．6
C．
D．
8、设是正数等差数列，
是正数等比数列，且a1=b1，a2n+1=b2n+1，则（ ）
A．an+1=bn+1 B．an+1＞bn+1 C．an+1＜bn+1 D．an+1≥bn+1
9、不等式
对一切
R恒成立，则实数a的取值范围是（ ）
A．（－
，－2） B．（－２，２） C．
D．（－ ，－２］
10、已知A、B、C是△ABC的三个内角，且
，则 （ ）
A．B=C B．B＞C C．B＜C D．B,C的大小与A的值有关
11、在△ABC中，如果
，那么cosC等于
（ ）
12、给出下列三个命题：
（1）若tanAtanB>1，则△ABC一定是钝角三角形；
（2）若sin2A＋sin2B＝sin2C，则△ABC一定是直角三角形；
（3）若cos(A－B)cos(B－C)cos(C－A)＝1，则△ABC一定是等边三角形
以上正确命题的个数有 （ ）
A．0个 B．1个 C．2个 D．3个
二、填空题（本大题共6小题，每小题５分，满分３０分）
13．在等差数列｛an｝中，已知公差d=
，且a1+a3+a5+…+a99=60，则a1+a2+a3+…+a99+a100=______________．
14．已知平面平域D由下列约束条件确定：2x-3y+5≥0,x+2y-8≤0,x-5y+6≥0,当点(x,y)在D上时，若z=3x-4y,则z的最小值是_______________．
15．设等比数列｛an｝共有3n项，它的前2n项的和为100，后2n项之和为200，则该等比数列中间n项的和等于___________________．
16．设
，则函数
的最小值是
．
17．在△ABC中，若
，则B等于_____________．
18．等差数列｛an｝中，Sn是它的前n项之和，且S6＜S7，S7＞S8，则
①等差数列的公差d＜0 ②S9一定小于S6
③a7是各项中最大的一项 ④S7一定是Sn中的最大值
其中正确的是_______________________（填入你认为正确的所有序号）
三、解答题（本大题共5小题，共７０分，解答应写出必要的文字说明、证明过程和演算步骤）
19、(本题满分12分)
若不等式
的解集是
，求不等式
的解集．
20、(本题满分1４分)
(1)已知
，求函数
的最大值．
(2)已知
且
，求
的最小值．
21、(本题满分14分)
设数列{
}的前
项和为
，已知
(1)试判断数列{}是否为等比数列，并加以证明；
(2)求和：
．
22、（本小题满分15分）
△ABC的三个内角A、B、C对边分别是a, b, c，且
，
，又△ABC的面积为
. 求（1）角C；（2）a+b的值．
23、（本题满分15分）
小华准备购买一台价值6000元的电脑，但现款不够，商场允许分期付款，但必须在一年内将款全部付清，商场提供了两种付款方案，供小华选择：
| 方案类别 | 分几次付清 | 付款方法 | 计息方法 | 月利率 |
| 1 | 6次 | 购买后2个月第一次付款,再过2个月第2次付款,---购买后12个月第6次付款 | 不计复利 | 1% |
| 2 | 12次 | 购买后1个月第一次付款,再过1个月第2次付款,---购买后12个月第12次付款 | 按复利计息 | 0.8% |
(1) 采用方案1，每期应付款多少？付款总额是多少？（精确到元）
(2) 采用方案2，每期应付款多少？付款总额是多少？（参考数据：
）
答题卷
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题：
13、___________________________． 14、________________________________．
15、___________________________． 16、________________________________．
17、___________________________． 18、________________________________．
三、解答题：
19、（12分）
20、（14分）
21、（14分）
22、（14分）
23、（16分）
 |
参考答案
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | B | A | C | D | D | C | D | C | A | D | C |
二、填空题：
13、145．
14、
． 15、
．
16、6．
17、
或
． 18、①②④．
三、解答题：
19解：∵不等式
的解集是
∴
且
∴
则不等式即为
故不等式的解集是
∣
20、（1）由知
，∴
则
取等号时
，∴
（2）∵且
∴
取等号时
故
21、（1）当
时，
当
时，
显然
也满足该式 ∴
由
（定值）∴ 
是等比数列．
（2）令T=
=
①
则
2T= 
②
由①－②得 －Ｔ=
=
=
∴Ｔ=
即=
22、（1）由
得
即
又
，∴
（2）
又
而
∴ 
23、（1）采用方案1，设每期付款
元，则
=
（元）
∴付款总额
（元）
（2）采用方案2，设每期付款元，则
∴
（元）
∴付款总额为
（元）