高一数学平面向量的应用举例测试

2．5平面向量的应用举例

班级　　　　 学号　　　　姓名　　　　 .

一选择题

1．已知A、B、C为三个不共线的点，P为△ABC所在平面内一点，若，则点P与△ABC的位置关系是　　　　　　　　　　　　　　　　　　　　　　  （　  ）

 A、点P在△ABC内部　　　　　　　　　  B、点P在△ABC外部

C、点P在直线AB上　　　　　　　　　　 D、点P在AC边上

2．已知三点A（1，2），B（4，1），C（0，-1）则△ABC的形状为　　　　　  （　  ）

 A、正三角形　　　B、钝角三角形　　 C、等腰直角三角形　　 D、等腰锐角三角形

3．当两人提起重量为G的旅行包时，夹角为，两人用力都为F，若F=G，则的值为（ ）

 A、30⁰　　　　B、60⁰　　　 C、90⁰　　　 D、120⁰

4．某人顺风匀速行走速度大小为a，方向与风速相同，此时风速大小为v，则此人实际感到的风速为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

 A、v-a　　　B、a-v　　 C、v+a　　 D、v

二、填空题

5．一艘船以5km/h的速度向垂直于对岸方向行驶，船的实际航行方向与水流方向成30⁰角，则水流速度为　　　　　　 km/h。

6．两个粒子a，b从同一粒子源发射出来，在某一时刻，以粒子源为原点，它们的位移分别为S_a=（3，-4），S_b=（4，3），（1）此时粒子b相对于粒子a的位移　　　　　　　 ；

（2）求S在S_a方向上的投影　　　　　　 。

三、解答题

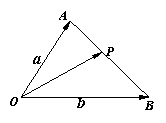
7．如图，点P是线段AB上的一点，且AP︰PB=︰，点O是直线AB外一点，设，，试用的运算式表示向量．

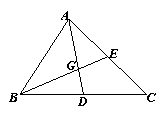
8．如图，△ABC中，D，E分别是BC，AC的中点，设AD与BE相交于G，求证：AG︰GD=BG︰GE=2︰1．

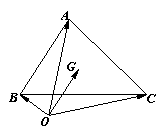
9．如图， O是△ABC外任一点，若，求证：G是△ABC重心（即三条边上中线的交点）．

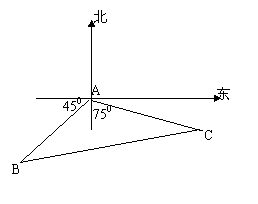10．一只渔船在航行中遇险，发出求救警报，在遇险地西南方向10mile处有一只货船收到警报立即侦察，发现遇险渔船沿南偏东75⁰，以9mile/h的速度向前航行，货船以21mile/h的速度前往营救，并在最短时间内与渔船靠近，求货的位移。