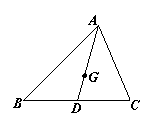
2．2．1向量加法运算及其几何意义
班级 学号 姓名 .
一、选择题
1．若C是线段AB的中点，则
（ ）
A．
B．
C．
D．以上均不正确
2．已知正方形ABCD边长为1，
，
，
，则
的模等于
A．0 B．3 C．
D．
（ ）
3．在四边形ABCD中，
，则四边形是
（ ）
A．矩形 B．菱形 C．正方形 D．平行四边形
4．向量
化简后等于
（ ）
A．
B． C．
D．
5．
、
为非零向量，且
，则
（ ）
A．与方向相同 B．
C．
D．与方向相反
6．设
，而是一非零向量，则下列各结论：①
；②
；③
；④
，其中正确的是
（ ）
A．①② B．③④ C．②④ D．①③
二、填空题
7．化简（
= 。
8．在矩形ABCD中，若
，
，则
_________。
9．已知
，
，∠AOB=60
，则
__________。
10．当非零向量和满足条件
时，使得
平分
和
间的夹角。
三、解答题
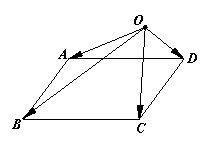
11．O是平行四边形ABCD外一点，求证：
。
12．一汽车向北行驶3 km，然后向北偏东60方向行驶3 km，求汽车的位移。
2．2．2向量减法运算及其几何意义
班级 学号 姓名 .
一选择题
1．化简
所得结果是
（ ）
A．
B．
C． D．
2．在
ABC中，
，则
的值为 （ ）
A．0 B．1 C．
D．2
3．设
和的长度均为6，夹角为 120，则
等于
（ ）
A．36 B．12 C．6 D．
4．下面四个式子中不能化简成
的是
（ ）
A．
B．
C．
D． 
5．3．在△ABC中，D、E、F分别BC、CA、AB的中点，点M是△ABC的重心，则
等于
（ ）
A．
B．
C．
D．
6．已知向量
反向，下列等式中成立的是 （ ）
A．
B．
C．
D．
二、填空题
7．在
ABCD中，，
，则
，
。
8．在=“向北走20km”，=“向西走15km”，则
=_________，
与的夹角的余弦值=______________。
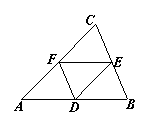
9．如图，D、E、F分别是ABC边AB、BC、CA上的
中点，则等式：
①
②
③
④
其中正确的题号是__________________
其中正确的题号是__________________
10．已知
、
是非零向量，指出下列等式成立的条件：
①
成立的条件是_________________________；
②
成立的条件是_________________________；
③
成立的条件是 _________________________；
④
成立的条件是_________________________。
三、解答题
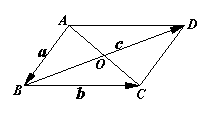
11．如图，O是ABCD的对角线AC与BD的交点，若，
，
，证明：
。
12．已知长度相等的三个非零向量、、
满足
，
求每两个向量之间的夹角。
2．2．3向量数乘运算及其几何意义
班级 学号 姓名 .
一选择题
1．化简
的结果是 （ ）
A．
B．
C．
D．
2．已知
，则下列命题正确的是
（ ）
A．
B．
C．
D．
3．下列各式计算正确的有 （ ）
(1)(－7)6a=-42a (2)7(a+b)－8b=7a+15b
(3)a－2b+a+2b=2a (4)若a=m+n,b=4m+4n,则a∥b
A．1个 B．2个 C．3个 D．4个
4．已知E、F分别为四边形ABCD的边CD、BC边上的中点，设
，
，则
=
A．
B．
C．
D．
（ ）
5．若
化简
（ ）
A． B． C．
D． 以上都不对
6．已知四边形ABCD是菱形，点P在对角线AC上（不包括端点A、C），则
=
（ ）
A．
B．
C． 
D． 
二、填空题
7．已知
、
是实数，、是向量，对于命题：
①
②
③若
，则
④若
，则
其中正确命题为_____________________．
8．计算：
（1）
=__________；
（2）
=__________．
9．已知向量，，且
，则
=__________．
10．若向量、
满足
，、为已知向量，则
=__________； =___________．
三、解答题
11．已知
，
是两个不共线的向量，
，
．若与是共线向量，求实数
的值．
12．如图，在ABC中，G是ABC的重心，证明：
