(数学1必修)第一章(下) 函数的基本性质
[提高训练C组]
一、选择题
1![]() 已知函数
已知函数![]() ,
,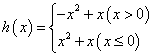 ,则
,则![]() 的奇偶性依次为( )
的奇偶性依次为( )
A![]() 偶函数,奇函数
B
偶函数,奇函数
B![]() 奇函数,偶函数
奇函数,偶函数
C![]() 偶函数,偶函数 D
偶函数,偶函数 D![]() 奇函数,奇函数
奇函数,奇函数
2![]() 若
若![]() 是偶函数,其定义域为
是偶函数,其定义域为![]() ,且在
,且在![]() 上是减函数,则
上是减函数,则![]() 的大小关系是( )
的大小关系是( )
A![]()
![]() >
>![]() B
B![]()
![]() <
<![]()
C![]()
![]()
![]()
![]() D
D![]()
![]()
![]()
![]()
3![]() 已知
已知![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的范围是( )
的范围是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4![]() 设
设![]() 是奇函数,且在
是奇函数,且在![]() 内是增函数,又
内是增函数,又![]() ,
,
则![]() 的解集是( )
的解集是( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
5![]() 已知
已知![]() 其中
其中![]() 为常数,若
为常数,若![]() ,则
,则![]() 的值等于( )
的值等于( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
6![]() 函数
函数![]() ,则下列坐标表示的点一定在函数f(x)图象上的是( )
,则下列坐标表示的点一定在函数f(x)图象上的是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
二、填空题
1![]() 设
设![]() 是
是![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() ,
,
则当![]() 时
时![]() _____________________
_____________________![]()
2![]() 若函数
若函数![]() 在
在![]() 上为增函数,则实数
上为增函数,则实数![]() 的取值范围是
的取值范围是 ![]()
3![]() 已知
已知![]() ,那么
,那么![]() =_____
=_____![]()
4![]() 若
若![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的取值范围是
的取值范围是
![]()
5![]() 函数
函数![]() 的值域为____________
的值域为____________![]()
三、解答题
1![]() 已知函数
已知函数![]() 的定义域是
的定义域是![]() ,且满足
,且满足![]() ,
,![]() ,如果对于
,如果对于![]() ,都有
,都有![]() ,
,
(1)求![]() ;
;
(2)解不等式![]()
![]()
![]()
2![]() 当
当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]()
3![]() 已知
已知![]() 在区间
在区间![]() 内有一最大值
内有一最大值![]() ,求
,求![]() 的值
的值![]()
4![]() 已知函数
已知函数![]() 的最大值不大于
的最大值不大于![]() ,又当
,又当![]() ,求
,求![]() 的值
的值![]()
(数学1必修)第一章(下) [提高训练C组]
参考答案
一、选择题
1![]() D
D
![]() ,
,
画出![]() 的图象可观察到它关于原点对称
的图象可观察到它关于原点对称
或当![]() 时,
时,![]() ,则
,则![]()
当![]() 时,
时,![]() ,则
,则![]()
![]()
2![]() C
C ![]() ,
,![]()
3![]() B
对称轴
B
对称轴![]()
4![]() D
由
D
由![]() 得
得![]() 或
或![]() 而
而![]()
即![]() 或
或![]()
5![]() D 令
D 令![]() ,则
,则![]() 为奇函数
为奇函数
![]()
6![]() B
B ![]() 为偶函数
为偶函数
![]() 一定在图象上,而
一定在图象上,而![]() ,∴
,∴![]() 一定在图象上
一定在图象上
二、填空题
1![]()
![]() 设
设![]() ,则
,则![]() ,
,![]()
∵![]() ∴
∴![]()
2![]()
![]() 且
且![]() 画出图象,考虑开口向上向下和左右平移
画出图象,考虑开口向上向下和左右平移
3![]()
![]()
![]() ,
,![]()
![]()
4![]()
![]() 设
设![]() 则
则![]() ,而
,而![]()
![]() ,则
,则![]()
5![]()
![]() 区间
区间![]() 是函数
是函数![]() 的递减区间,把
的递减区间,把![]() 分别代入得最大、小值
分别代入得最大、小值
三、解答题
1. 解:(1)令![]() ,则
,则![]()
(2)![]()
![]()
![]() ,
,![]()
则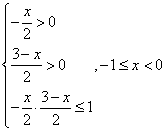
![]()
2. 解:对称轴![]()
当![]() ,即
,即![]() 时,
时,![]() 是
是![]() 的递增区间,
的递增区间,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() 是
是![]() 的递减区间,
的递减区间,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]()
![]()
3![]() 解:对称轴
解:对称轴![]() ,当
,当![]() 即
即![]() 时,
时,![]() 是
是![]() 的递减区间,
的递减区间,
则![]() ,得
,得![]() 或
或![]() ,而
,而![]() ,即
,即![]() ;
;
当![]() 即
即![]() 时,
时,![]() 是
是![]() 的递增区间,则
的递增区间,则![]() ,
,
得![]() 或
或![]() ,而
,而![]() ,即
,即![]() 不存在;当
不存在;当![]() 即
即![]() 时,
时,
则![]() ,即
,即![]() ;∴
;∴![]() 或
或 ![]()
![]()
4![]() 解:
解:![]() ,
,
对称轴![]() ,当
,当![]() 时,
时,![]() 是
是![]() 的递减区间,而
的递减区间,而![]() ,
,
即![]() 与
与![]() 矛盾,即不存在;
矛盾,即不存在;
当![]() 时,对称轴
时,对称轴![]() ,而
,而![]() ,且
,且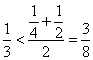
即![]() ,而
,而![]() ,即
,即![]()
∴![]()