(数学1必修)第一章(下) 函数的基本性质
[综合训练B组]
一、选择题
1![]() 下列判断正确的是( )
下列判断正确的是( )
A![]() 函数
函数![]() 是奇函数
B
是奇函数
B![]() 函数
函数![]() 是偶函数
是偶函数
C![]() 函数
函数![]() 是非奇非偶函数 D
是非奇非偶函数 D![]() 函数
函数![]() 既是奇函数又是偶函数
既是奇函数又是偶函数
2![]() 若函数
若函数![]() 在
在![]() 上是单调函数,则
上是单调函数,则![]() 的取值范围是( )
的取值范围是( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
3![]() 函数
函数![]() 的值域为( )
的值域为( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
4![]() 已知函数
已知函数![]() 在区间
在区间![]() 上是减函数,
上是减函数,
则实数![]() 的取值范围是( )
的取值范围是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5![]() 下列四个命题:(1)函数
下列四个命题:(1)函数![]() 在
在![]() 时是增函数,
时是增函数,![]() 也是增函数,所以
也是增函数,所以![]() 是增函数;(2)若函数
是增函数;(2)若函数![]() 与
与![]() 轴没有交点,则
轴没有交点,则![]() 且
且![]() ;(3)
;(3) ![]() 的递增区间为
的递增区间为![]() ;(4)
;(4) ![]() 和
和![]() 表示相等函数
表示相等函数![]()
其中正确命题的个数是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
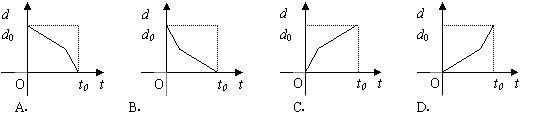 |
6
二、填空题
1![]() 函数
函数![]() 的单调递减区间是____________________
的单调递减区间是____________________![]()
2![]() 已知定义在
已知定义在![]() 上的奇函数
上的奇函数![]() ,当
,当![]() 时,
时,![]() ,
,
那么![]() 时,
时,![]()
![]()
3![]() 若函数
若函数![]() 在
在![]() 上是奇函数,则
上是奇函数,则![]() 的解析式为________
的解析式为________![]()
4![]() 奇函数
奇函数![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上的最大值为
上的最大值为![]() ,
,
最小值为![]() ,则
,则![]() __________
__________![]()
5![]() 若函数
若函数![]() 在
在![]() 上是减函数,则
上是减函数,则![]() 的取值范围为__________
的取值范围为__________![]()
三、解答题
1![]() 判断下列函数的奇偶性
判断下列函数的奇偶性
(1)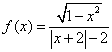 (2)
(2)![]()
2![]() 已知函数
已知函数![]() 的定义域为
的定义域为![]() ,且对任意
,且对任意![]() ,都有
,都有![]() ,且当
,且当![]() 时,
时,![]() 恒成立,证明:(1)函数
恒成立,证明:(1)函数![]() 是
是![]() 上的减函数;
上的减函数;
(2)函数![]() 是奇函数
是奇函数![]()
3![]() 设函数
设函数![]() 与
与![]() 的定义域是
的定义域是![]() 且
且![]() ,
,![]() 是偶函数,
是偶函数, ![]() 是奇函数,且
是奇函数,且![]() ,求
,求![]() 和
和![]() 的解析式
的解析式![]()
4![]() 设
设![]() 为实数,函数
为实数,函数![]() ,
,![]()
(1)讨论![]() 的奇偶性;
的奇偶性;
(2)求![]() 的最小值
的最小值![]()
(数学1必修)第一章(下) [综合训练B组]
参考答案
一、选择题
1![]() C
选项A中的
C
选项A中的![]() 而
而![]() 有意义,非关于原点对称,选项B中的
有意义,非关于原点对称,选项B中的![]()
而![]() 有意义,非关于原点对称,选项D中的函数仅为偶函数;
有意义,非关于原点对称,选项D中的函数仅为偶函数;
2![]() C
对称轴
C
对称轴![]() ,则
,则![]() ,或
,或![]() ,得
,得![]() ,或
,或![]()
3![]() B
B ![]() ,
,![]() 是
是![]() 的减函数,
的减函数,
当![]()
4![]() A 对称轴
A 对称轴![]()
1. A (1)反例![]() ;(2)不一定
;(2)不一定![]() ,开口向下也可;(3)画出图象
,开口向下也可;(3)画出图象
可知,递增区间有![]() 和
和![]() ;(4)对应法则不同
;(4)对应法则不同
6![]() B 刚刚开始时,离学校最远,取最大值,先跑步,图象下降得快!
B 刚刚开始时,离学校最远,取最大值,先跑步,图象下降得快!
二、填空题
1![]()
![]() 画出图象
画出图象
2![]()
![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ∴
∴![]() ,
,![]()
3![]()
![]()
∵![]() ∴
∴![]()
即![]()
4![]()
![]()
![]() 在区间
在区间![]() 上也为递增函数,即
上也为递增函数,即![]()
![]()
5![]()
![]()
![]()
三、解答题
1![]() 解:(1)定义域为
解:(1)定义域为![]() ,则
,则![]() ,
,![]()
∵![]() ∴
∴![]() 为奇函数
为奇函数![]()
(2)∵![]() 且
且![]() ∴
∴![]() 既是奇函数又是偶函数
既是奇函数又是偶函数![]()
2![]() 证明:(1)设
证明:(1)设![]() ,则
,则![]() ,而
,而![]()
∴![]()
∴函数![]() 是
是![]() 上的减函数;
上的减函数;
(2)由![]() 得
得![]()
即![]() ,而
,而![]()
∴![]() ,即函数
,即函数![]() 是奇函数
是奇函数![]()
3![]() 解:∵
解:∵![]() 是偶函数,
是偶函数, ![]() 是奇函数,∴
是奇函数,∴![]() ,且
,且![]()
而![]() ,得
,得![]() ,
,
即![]() ,
,
∴![]() ,
,![]()
![]()
4![]() 解:(1)当
解:(1)当![]() 时,
时,![]() 为偶函数,
为偶函数,
当![]() 时,
时,![]() 为非奇非偶函数;
为非奇非偶函数;
(2)当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 不存在;
不存在;
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]()