高一数学下学期同步测试3

　 高一数学下学期同步测试（3）—1.1空间几何体

本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.

第Ⅰ卷（选择题，共50分）

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．

1．过正三棱柱底面一边的截面是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．三角形　　 　　　　　　　　　　　　　　　　　　　B．三角形或梯形　　

C．不是梯形的四边形　　　　　　　　　　　　　　 D．梯形

2．若正棱锥底面边长与侧棱长相等，则该棱锥一定不是　　　　　　　　　　　　　　　　　　　　（　　）

　  A．三棱锥 　　　　　　　B．四棱锥　　　　　　　　C．五棱锥　　　　　　　 D．六棱锥

3．球的体积与其表面积的数值相等，则球的半径等于　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　 　　　　　　 B．1　　　　　　　　　　C．2　　 　　　　　　　 D．3

4．将一个边长为a的正方体，切成27个全等的小正方体，则表面积增加了　　　　　 （　　）

　　　 A．　　 　　　　　B．12a²　　　　　　　　　　C．18a²　　　　　　　　　 D．24a²

5．直三棱柱各侧棱和底面边长均为a，点D是CC′上任意一点，连结A′B，BD，A′D，AD，则三棱锥A—A′BD的体积　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　 D．

6．两个球体积之和为12π，且这两个球大圆周长之和为6π，那么这两球半径之差是（　　）

　　　　 A． 　　　　　　　　　　B．1　　　　　　　　　　　 C．2　 　　　　　　　　　 D．3

7．一个球与它的外切圆柱、外切等边圆锥（圆锥的轴截面为正三角形）的体积之比（　　）

A．2：3：5 　　　　　　B．2：3：4 　　　　　　C．3：5：8　　　　　　　D．4：6：9

8．直径为10cm的一个大金属球，熔化后铸成若干个直径为2cm的削球，如果不计损耗，可

　 铸成这样的小球的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．5　 　　　　　　　　　 B．15　　　　　　　　　　 C．25　　　　　　　　　　　D．125

9．与正方体各面都相切的球，它的表面积与正方体的表面积之比为　　　　　　　　　　　 （　　）

A．　　　　  　　B．　　  　　　　　 C．　　　　　　　　　 D．

10．中心角为135°的扇形，其面积为B，其围成的圆锥的全面积为A，则A：B为（　　）

　　　 A．11：8　　　　　　　　B．3：8　　 　　　　　C．8：3 　　　　　　　　 D．13：8

第Ⅱ卷（非选择题，共100分）

二、填空题：请把答案填在题中横线上（每小题6分，共24分）．

11．直平行六面体的底面是菱形，两个对角面面积分别为，直平行六面体的侧面积为_____________．

12．正六棱锥的高为4cm，最长的对角线为cm，则它的侧面积为_________．

13．球的表面积扩大为原来的4倍，则它的体积扩大为原来的___________倍．

14．已知正三棱锥的侧面积为18 cm,高为3cm. 求它的体积　　　　  ．

三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．

15．（12分）

　　　 ①轴截面是正方形的圆柱叫等边圆柱．

　　　　　 已知：等边圆柱的底面半径为r，求：全面积；

　　　 ②轴截面是正三角形的圆锥叫等边圆锥.

　　　　　 已知：等边圆锥底面半径为r，求：全面积．

16．（12分）四边形，绕y轴旋转一周，求所得

　　旋转体的体积．

17．（12分）如图，圆锥形封闭容器，高为h，圆锥内水面高为若将圆锥倒置后，

　　圆锥内水面高为

18．（12分）如图，三棱柱 上一点，求 ．

19．（14分）如图，在正四棱台内，以小底为底面。大底面中心为顶点作一内接棱锥. 已知棱台小底面边长为b，大底面边长为a，并且棱台的侧面积与内接棱锥的侧面面积相等，求这个棱锥的高，并指出有解的条件．

20．（14分）已知：一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱．

　 （1）求圆柱的侧面积；

　 （2）x为何值时，圆柱的侧面积最大．

参考答案（三）

一、BDDBC　 BDDBA

二、11．；　　12． cm；　 13．8；　 14．cm³.

三、15．①解：

　　　　　　　　　　　　　

　　　　 ②解：

　　　　　　　　　　　　　　

16．解：

　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　

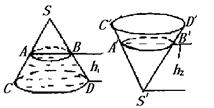
17．分析：圆锥正置与倒置时，水的体积不变，另外水面是平行于底面的平面，此平面截得的小圆锥与原圆锥成相似体，它们的体积之比为对应高的立方比.

　　　 解：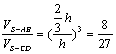

　　　　　　　　　　　　　　　　　　　

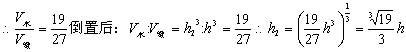
　　　 小结：此题若用 计算是比较麻烦的，因为台体的上底面半径还需用导出来，我们用 的体积之间有比例关系，可以直接求出.

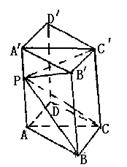
18．解法一：设 的距离为

　　　 把三棱柱 为相邻侧面的平行六面体，此平行六面体体积为原三棱柱体积的两倍.

　　　

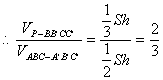
　　　 解法二：

　　　

　　　

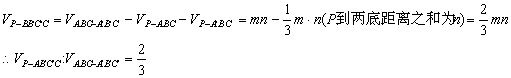
　　　　 小结：把三棱柱接补成平行六面体是重要的变换方法，平行六面体的每一个面都可以当作柱体的底，有利于体积变换.

19．分析：这是一个棱台与棱锥的组合体问题，也是立体几何常见的问题，这类问题的图形往往比较复杂，要认真分析各有关量的位置和大小关系，因为它们的各量之间的关系较密切，所以常引入方程、函数的知识去解.

　　　　 解：如图，过高的中点E作棱锥和棱台的截面，得棱台的斜高EE₁和棱锥的斜高为EO₁，设，所以

　　　

　　　 ①式两边平方，把②代入得：

　　　

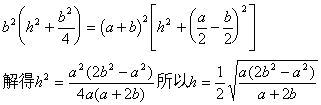
　　　　 显然，由于，所以此题当且仅当时才有解.

　　　 小结：在棱台的问题中，如果与棱台的斜高有关，则常应用通过高和斜高的截面，如果和棱台的侧棱有关，则需要应用通过侧棱和高的截面，要熟悉这些截面中直角梯形的各元素，进而将这些元素归结为直角三角形的各元素间的运算，这是解棱台计算问题的基本技能之一.

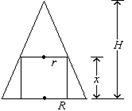20．解：（1）设内接圆柱底面半径为r.

　　　

　　　 ②代入①

　　　　

　　（2）
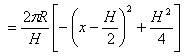