高一数学下学期同步测试（6）—2.1平面直角坐标系中的基本公式
YCY
本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.
第Ⅰ卷（选择题，共50分）
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．
1．关于位移向量说法正确的是 （ ）
A．数轴上任意一个点的坐标有正负和大小，它是一个位移向量；
B．两个相等的向量的起点可以不同；
C．每一个实数都对应数轴上的唯一的一个位移向量；
D．
的大小是数轴上A、B两点到原点距离之差的绝对值。
2．化简
等于 （ ）
A．
B．零位移 C．
D． 
3． 若
，
（其中
），向量的最小值 （ ）
A．
B．0 C．
D．
4．数轴上到
，
两点距离之和等于1的点的集合为 （ ）
A．{0，3} B．{0，1，2，3} C．{1，2} D．
5．方程
的解为 （ ）
A．
B．
C．
D．
6．已知
，
，则
的垂直平分线方程为 （ ）
A．
B．
C．
D．
7．以
为顶点的三角形是 （ ）
A．直角三角形 B．等腰三角形 C．正三角形 D． 等腰直角三角形
8．已知三点
在同一直线上，则实数
的值是 （ ）
A．1 B．4 C．3 D．不确定
9．在直线
到
距离最短的点是 （ ）
A．（0，0） B．（1，1） C．（－1，－1） D．（
）
10．
轴上点到
两点距离的最小值为 （ ）
A．3 B．
C．5 D．17
第Ⅱ卷（非选择题，共100分）
二、填空题：请把答案填在题中横线上（每小题6分，共24分）．
11．若点
与点
的距离为5，则
．
12．若
，点
是的垂直平分线上一点，则
___________．
13．若
，则
___ __．
14．直线
上的两点的横坐标分别为
，则两点间的距离为____________；直线上的两点的纵坐标分别为
，则两点间的距离为
．
三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．
15．（12分）已知点
，在轴上找一点使得
，并求出
的值．
16．（12分）已知点
与
间的距离为
，求的值．
17．（12分）已知点P (x, y)，则求①关于y轴的对称点；②关于x轴的对称点；③关于原点的对称点；④关于直线y = x的对称点；⑤关于直线y=－x的对称点(－y, －x)．
18．（12分）判断下列A（－1，－1），B（0，1），C（1，3）三点是否共线，并给出证明．
19．（14分）用坐标法证明三角形的中位线长为其对应边长的一半．
20．（14分）已知一条曲线在x轴的上方，它上面的每一点到点A（0，2）的距离减去它到x轴的距离的差都是2，求这条曲线的方程．
参考答案（六）
一、BCDDA BBCAC．
二、11．0或8；12．
；13．
；14．
，
；
三、15．解：设
，则有
； 
；
由
可得
；
解得
，从而得
，且
.
16．解： 由
又由
即
，得
或
.
17．解： ①(－x, y)；②(x, －y)；③(－x, －y)；④(y, x)；⑤(－y, －x).
18．解：三点共线. 
； 
；
；则
，所以三点共线.
19．证： 只需将三角形三个顶点的坐标设出，再利用中点坐标公式，求出两腰中点的坐标. 最后用两点间距离公式求得结果既可.
20．解：解：设点M（x,y）是曲线上任意一点，MB⊥x轴，垂足是B，那么点M属于集合
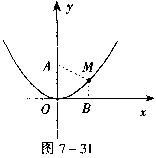
由距离公式，点M适合的条件可表示为：
①
将①式移项后再两边平方，得x2+(y－2)2=(y+2)2,
| |
因为曲线在x轴的上方，所以y＞0,虽然原点O的坐标（0，0）是这个方程的解，但不属于已知曲线，所以曲线的方程是
(x≠0) ,它的图形是关于y轴对称的抛物线，但不包括抛物线的顶点，如图所示.