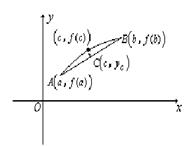高一数学下学期同步测试（7）—2.2直线方程
YCY
本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.
第Ⅰ卷（选择题，共50分）
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．
1．经过点
和
的直线的斜率等于1，则
的值是 （ ）
A．4 B．1 C．1或3 D．1或4
2．若方程
表示一条直线，则实数满足 （ ）
A．
B．
C．
D．，，
3．直线l与两直线y＝1和x－y－7＝0分别交于A，B两点，若线段AB的中点为
M（1，－1），则直线l的斜率为 （ ）
A．
B．
C．－ D． －
4．△ABC中，点A(4，－1),AB的中点为M(3，2),重心为P(4，2)，则边BC的长为（ ）
A．5 B．4 C．10 D．8
5．直线kx－y＋1＝3k，当k变动时，所有直线都通过定点 （ ）
A．(0，0) B．(0，1) C．(3，1) D．(2，1)
6．如果AC＜0且BC＜0，那么直线Ax＋By＋C＝0不通过 （ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
7．下列说法的正确的是 （ ）
A．经过定点
的直线都可以用方程
表示
B．经过定点
的直线都可以用方程
表示
C．不经过原点的直线都可以用方程
表示
D．经过任意两个不同的点
的直线都可以用方程
表示
8．如果直线l沿x轴负方向平移3个单位再沿y轴正方向平移1个单位后，又回到原来的位
置，那么直线l的斜率是 （ ）
A．
B．－3 C．
D．3
9．直线
在
轴上的截距是 （ ）
A．
B．－
C． D．
10．若
都在直线
上，则
用
表示为 （ ）
A．
B．
C．
D． 
第Ⅱ卷（非选择题，共100分）
二、填空题：请把答案填在题中横线上（每小题6分，共24分）．
11．直线l过原点，且平分□ABCD的面积，若B(1, 4)、D(5, 0)，则直线l的方程
是 ．
12．一直线过点（－3，4），并且在两坐标轴上截距之和为12，这条直线方程是_____ _____．
13．若方程
表示两条直线，则的取值是
．
14．当
时，两条直线
、
的交点在
象限．
三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．
15．（12分）
已知直线
，
（1）系数为什么值时，方程表示通过原点的直线；
（2）系数满足什么关系时与坐标轴都相交；
（3）系数满足什么条件时只与x轴相交；
（4）系数满足什么条件时是x轴；
（5）设
为直线上一点，
证明：这条直线的方程可以写成
．
16．（12分）过点
作一直线l，使它与两坐标轴相交且与两轴所围成的三角形面积为5．
|
在
及
之间的一段图象近似地看作直线，设
，证明：
的近似值是：
．
18．（12分）已知：A（－8，－6），B（－3，－1）和C（5，7），求证：A，B，C三点共线．
19．（14分）
的三个顶点是O（0，0），A（1，0），B（0，1）. 如果直线l： 将三角形OAB的面积分成相等的两部分，且
.求
和b应满足的关系．
20．（14分）已知
中，A(1, 3)，AB、AC边上的中线所在直线方程分别为
和
，求各边所在直线方程．
参考答案（七）
一、BCDAC CDABD．
二、11．
；12．
或
；13．
；14．二；
三、15．解：（1）采用“代点法”，将O（0，0）代入
中得C=0，A、B不同为零.
（2）直线
与坐标轴都相交，说明横纵截距
均存在.设
，得
；
设
，得
均成立，因此系数A、B应均不为零.
（3）直线只与x轴相交，就是指与y轴不相交——平行、重合均可。因此直线方程将化成
的形式，故
且
为所求.
（4）x轴的方程为，直线方程中
即可.注意B可以不为1，即
也可以等价转化为.
（5）运用“代点法”. 
在直线上，
满足方程， 即
，
故可化为
，
即
，得证.
16．分析：直线l应满足的两个条件是
（1）直线l过点（－5, －4）；（2）直线l与两坐标轴相交且与两轴所围成的三角形面积为5.
如果设a，b分别表示l在x轴，y轴上的截距，则有
.
这样就有如下两种不同的解题思路：
第一，利用条件（1）设出直线l的方程（点斜式），利用条件（2）确定；
第二，利用条件（2）设出直线l的方程（截距式），结合条件（1）确定a，b的值.
解法一：设直线l的方程为
分别令
，
得l在x轴，y轴上的截距为：
，
由条件（2）得
得
无实数解；或
，解得
故所求的直线方程为：
或
解法二：设l的方程为
，因为l经过点
，则有：
① 又
②
联立①、②，得方程组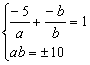
解得
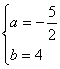或
因此，所求直线方程为：或.
17．证明：设线段AB上点
，函数
的图象上相应点为
由
，知
解得，
依题意，
的近似值是
.
18．证明一：由A，B两点确定的直线方程为：
即：
①
把C（5，7）代入方程①的左边：左边
右边
∴C点坐标满足方程①∴C在直线AB上∴A，B，C三点共线
证明二：∵
|
∴A，B，C三点共线.
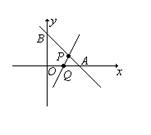
19． 解：设
和AB交于P，和x轴交于Q点，则
由
，有
依题意：
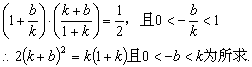
20．分析：B点应满足的两个条件是：①B在直线
上；②BA的中点D在直线
上。由①可设
，进而由②确定
值.
解：设则AB的中点
∵D在中线CD：上∴
，
解得
， 故B(5, 1).
同样，因点C在直线上，可以设C为
，求出
.
根据两点式，得
中AB：
， BC：
，AC：.