高一数学下期六月份阶段性测试题
时量:120分 总分:100分
一、选择题(本大题共12小题，每小题3分，满分36分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1、已知a=(3,－1),b=(－1,2),则－3a－2b等于
（A）（7，1） （B）（－７，－１） （Ｃ）（－７，１） （Ｄ）（７，－１）
2在函数
中，最小正周期为
的函数是
A．
B．
C．
D ．
3．若点P分有向线段
的比为
，则点P1分有向线段
所成的比为（ ）
A．
B．2 C．1 D．－1
4． 
的值等于 （ ）
A．
B．
C．
D．
5．已知
的面积为
，且
，
，则角
为(
)
（A）
（B）
（C）或
（D）或
6．在中，若
，则这个三角形为(
)
（A）直角三角形 （B）钝角三角形 （C）锐角三角形 （D）等腰三角形
7，已知┃
┃2=1,
┃
┃2=2, 
,则与的夹角为
(A)30º (B)45º (C)60º (D)90º
8、要得到函数y=sin(2x-
)的图象，只需要将y=sin2x的图象 （ ）
A 、向右平移
个单位 B、向左平移个单位
C、向右平移个单位
D、向左平移个单位
9. 设
，
，
，当
，且
时，点
在：
A．线段AB上 B．直线AB上
C．直线AB上，但除去A点 D．直线AB上，但除去B点
10、在△ABC中，已知tanA、tanB是方程3x2＋8x－1＝0的两个根，则tanC等于 （ ）
A．2 B．－2 C．4 D．－4
11、边长为
的正三角形ABC中，设
=c, 
=a, 
=b,则a·b+b·c+c·a等于（ ）
A．0 B．1 C．3 D．－3
12．如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点
向结点
传递信息，信息可以分开沿不同的路线同时传递.则单位时间内从结点向结点传递的最大信息量为
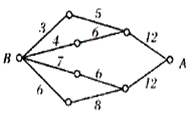（A）26 （B）24
（C）20 （D）19
二、填空题：本题共有4小题．只要求直接填写结果，每题4分，本题满分16分.
13、若向量
=(－1,x)与 
=(－x,2)共线，则 x= 。
14、点M（4，3）关于点N（5，－3）的对称点L的坐标是 。
15．若奇函数
满足
，
，则
。
16．在中，有命题
①
；②
；③若
，则为等腰三角形；④若
，则为锐角三角形.
上述命题正确的是
试题答卷
请把选择题答案填在下列表格内，每小题3分，共36分）
| 题号
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案二、填空题（共16分）
13、 14、
15、 16、
三：解答题
17、(本题满分6分) 已知=4,=3,当（1）⊥；（2）与的夹角为60º时，；（3） ∥ , 分别求 与 的数量积
18、(本题满分8分)已知 平面向量
，
．
（Ⅰ）证明： 
；
（Ⅱ）是否存在不同时为零的实数
和
，使
，
，且
．若存在，试求关于的函数关系式
，并求K的取值范围；若不存在，请说明理由．
19、(本题满分10分) 已知、、三点的坐标分别为
、
、
，
， （1）若
，求角
的值；
（2）若
，求
的值。
20．(本题满分10分)已知： 、、
是同一平面内的三个向量，其中=（1，2）
（Ⅰ）若
，且//，求的坐标；
（Ⅱ）若=
且
与2
垂直，求与的夹角θ.
21. （本小题满分8分） 在
中，a，b，c分别是
的对边长，已知a，b，c成等比数列，且
，求
的大小及
的值。
22.（本题满分6分）某港口水的深度y（米）是时间t（0≤t≤24，单位：时）的函数，记作y=f（t），下面是某日水深的数据：
| t（时） | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y（米） | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.1 |
经长期观察，y=f（t）的曲线可近似地看成函数
的图象.
（1）试根据以上数据，求出函数的最小正周期、振幅和表达式；
（2）一般情况下，船舶航行时，船底离海底距离为5米或5米以上时认为是安全的（船舶停靠时，船底只需不碰海底即可）.某船吃水深度（船底离水面的距离）为6.5米.如果该船希望在同一天内安全进出港，请问，它至多能在港内停留多长时间（忽略进出港所需的时间）?
  | |||
 | |||
参考答案
（请把选择题答案填在下列表格内，每小题3分，共36分）
| 题号
| 1 B | 2 A | 3 C | 4 C | 5 D | 6 A | 7 B | 8 A | 9 B | 10 A | 11 D | 12 D |
答案 
二、填空题：本题共有4小题．每题填对得3分，本题满分12分.
13、 x=
14. （ 6，-9 ） 。15. 5/2 
16。②③
三：解答题
17、(本题满分6分)
解：（1）：0，----2分（2）：6，――2分（3）12或-12――2 分
18、题解：（Ⅰ）略…………2分
（Ⅱ）由（Ⅰ）知：
，
…………4分
∴
…………6分
＝
―――8分
19解：（1）
，
（………………………1分）
由得
又
（………4分）
（2）由，得
（………………………7分）
又=
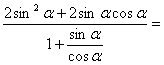
所以，=
。
（………………………10分）
20. 解：得出 y=2x, x2+y2=20 3分
（Ⅰ） ＝（2，4）或（-2，-4） 5分
（Ⅱ） ·＝-5/2，COSθ＝-1，θ＝1800 10分
21. 解：（I）
成等比数列 
1分
又 
在中，由余弦定理得
4分
（II）在中，由正弦定理得
8分
22.解:(1)由已知数据知,最小正周期T=12,则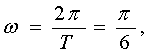
又振幅A=3,b=10
………………………………………………3分
(2) 由题意,该船进出港时,水深应不小于5+6.5=11.5米.
所以
解得
…
在同一天内,取k=0或1,所以
. 5分
故该船可在当日凌晨1时进港,17时离港,它至多能在港内停留16小时. 6分