解不等式
一．典型例题：
例1：解下列不等式
（1）
（2）
（3）
（4）
（5）
例2：解下列关于
的不等式
（1）
（2）
例3：已知不等式
的解集为
且
求不等式
的解集。
例4：方程
的两个根都在区间
内，
求实数
的取值范围。
二．巩固练习
1．不等式
的解集是
（ ）
A．R
B．空集
C. 
D. 
2．已知集合M=
，N=
，
则
为
（ ）
A．
或
B．
或
C．
或
D．
或
3．不等式
的解集为
（ ）
A．
或
B．
或
C．或
D.
或
4. 函数
的定义域为
（ ）
A. 
B.
C.
D.
5. 已知方程
的两个根都是正实数，
则实数
的取值范围
（ ）
A．
B.
C. 
D.
6. 不等式
的解集是
（ ）
A．
B．
C．
D．
7. 已知集合
，
,
则
的取值范围是
（ ）
A．
B.
C.
D.
8．不等式
的解是
，则不等式
的解为（ ）
A．
<
B．－
— 
C．－－ D．
9．函数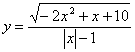
的定义域 .
10 . 已知
有意义，则实数的取值范围
11. 若不等式
对任意实数均成立，
则实数的取值范围
.
12. 不等式
的解集为
或
则实数的取值范围
.
13.下面4个关于不等式的命题：(1)若
，则
或
;
(2)若
，则不等式的解集为空集；(3)任意
，恒有
(4) 若
，则
。其中正确的命题是
.
14．解关于的不等式：
(1)
(2) 
15.若关于的不等式
的解为一切实数，求实数的取值范围
16.方程
的两个根，一个大于3，另一个小于3，
求实数
的取值范围。
部分答案：
例1：（1）
（2）
或
（3）或
（4）
或
（5）
或 
，或
例2（1）当
当
当
,解集为空集。
（2）当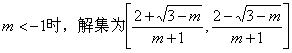
当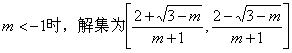
当
,解集为空集
例3: 
或
例4： 
巩固练习： AADCBBAC
9．
10. 
11. 
12. 
13. (2)
14．（1）
（2）当
当
当
时,解集为
。
15．
16．