前黄中学三角函数总练习 班学号 姓名
一、选择题
1、要得到函数
的图象，只需将y=cos3x的图像
（ ）
A、向右平移
B、向左平移 C、向右平移
D、向左平移
2、函数
的图像中的一条对称轴方程是
（ ）
A、
B、
C、
D、
3、函数
图像的对称中点是（ ）
A、
B、
C、
D、
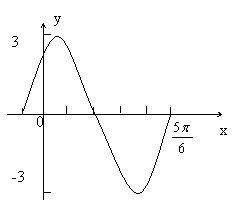4、函数y=Asin(ωx+φ)在一个同期内的图象如图，则y的表达式为 （ ）
A、
B、
|
D、
5、由函数图象可知，sin2x=sinx，在[0，2π]上实数解的个数是 （ ）
A、3个 B、4个 C、5个 D、6个
6、函数
的图象经过下列平移变换，就可得到函数y=5sin2x（ ）
A、向右平移
B、向左平移 C、向右平移
D、向左平移
7、函数y=tanx-cotx是 （ ）
A、奇函数 B、偶函数
C、既是奇函数又是偶函数 D、既不是奇函数又不是偶函数
8、已知函数f(x)=cot(2x-
)，下列判断正确的是
（ ）
A、f(x)是定义域上的减函数，周期为
B、f(x)是区间(0，π)上的减函数，周期为2π
C、f(x)是区间(
)上的减函数，周期是
D、f(x)是区间(
)上的减函数，周期为
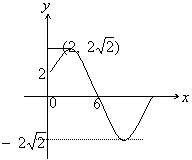
9、
的图象如图，则解析式是
（ ）
A、
B、
C、
D、
10、已知函数，在同一周期内，当
时，取得最大值2；当
时，取得最小值-2，那么这个函数解析式是
（ ）
A、
B、
C、 D、
11、观察正切曲线，满足tanx≤1的x取值范围是 （ ）
A、
B、
C、
D、
12、既是以π为周期的函数，又是在(0，)上为减函数的为
（ ）
A、
B、y=sinx C、y=-cos2x D、y=cotx
二、填空题
13、把函数y=sin(2x+)的图像向右平移
个单位，再将横坐标压缩到原来的
，所得到的函数图象的解析式是
。
14、函数y=Asin(ωx+φ)（A>0,ω>0,
）的最小值是-3，周期为，
且它们的图象经过点（0，
），则这个函数的解析式是
。
前黄中学三角函数总练习 班姓名
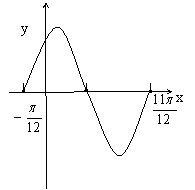15、已知函数y=2sin(ωx+φ)(φ<)的图象（如图），
那么φ= ，ω= 。
16、若函数y=tan(3ax-)(a≠0)的最小正周期为，
则a= 。
17、若α、β均在
内，且
，
则α+β的范围是 。
18、已知
，则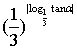
=
三、解答题
19、
ABC的三个内角为A、B、C,求当A为何值时,cosA+cos
取得最大值,并求出这个最大值
20、已知：
（
R，a为常数）．
（1）若
，求f（x）的最小正周期；
（2）若
，
时，f（x）的最大值为4，求a的值．
21．已知二次函数
对任意
，都有
成立，设向量
（sinx，2），
（2sinx，），
（cos2x，1），
（1，2），当
[0，
]时，求不等式f（
）＞f（
）的解集．
22、已知a＝（
，
），b＝（
，
），a与b之间有关系式ka+b=
a-kb，其中k＞0．
（1）用k表示a、b；
（2）求a·b的最小值，并求此时，a与b的夹角
的大小．
【前黄中学三角函数练习答案】
一、选择题
1、C 2、B 3、B 4、D 5、C 6、C 7、A 8、D
9、C 10、A 11、C 12、D
二、填空题
13、y=sin4x 14、
15、
16、
17、
18、cotα
三、解答题
19、
20、解析：∵ 
（1）最小正周期 
（2）
，
∴ 
时 
，∴ 
， ∴ a＝1．
21、解析：设f（x）的二次项系数为m，其图象上两点为（1-x，
）、B（1＋x，
）因为
，，所以
，由x的任意性得f（x）的图象关于直线x＝1对称，若m＞0，则x≥1时，f（x）是增函数，若m＜0，则x≥1时，f（x）是减函数．
∵ 
，
，
，
，
，
，
∴ 当
时，
，
．
∵ 
， ∴ 
．
当
时，同理可得
或
．
综上：
的解集是当时，为
；
当时，为
，或
．
22、解：由已知
．
∵ 
，
∴ 
．
∴ 
． ∵ k＞0， ∴ 
．
此时
∴ 
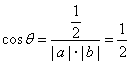． ∴ ＝60°．