高一数学复习——三角函数
班级 姓名
【复习要点】
1. 了解任意角的概念和弧度制;借助单位圆理解掌握三角函数的定义;理解同角三角函数的基本关系;熟练运用诱导公式。
2. 结合三角函数图象理解三角函数的性质(周期性,单调性,最大和最小值等)。
3. 结合![]() 的图象观察参数的变化对函数图象的影响;能应用三角函数解决一些简单的实际问题。
的图象观察参数的变化对函数图象的影响;能应用三角函数解决一些简单的实际问题。
【例题分析】
1.已知2弧度的圆心角所对的弧长为![]() ,则此圆心角所对的扇形面积是____________.
,则此圆心角所对的扇形面积是____________.
2.方程![]() 的实根个数为
.
的实根个数为
.
3.函数![]() 的定义域是
.
的定义域是
.
4.要得到![]() 的图象只要把
的图象只要把![]() 的图象
( )
的图象
( )
A. 右移 B. 左移 C. 右移 D. 左移
5.已知![]() 的值是 .
的值是 .
6.已知![]() .
.
(I)求sinx-cosx的值;
(Ⅱ)求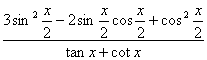 的值.
的值.
7.化简![]() 并求函数
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
8.函数![]() 的最小正周期是___________.
的最小正周期是___________.
9.设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() 。
。
(Ⅰ)求![]() ; (Ⅱ)求函数
; (Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
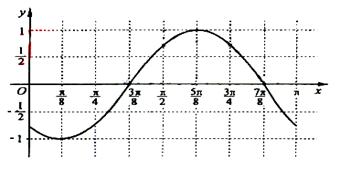
(Ⅲ)画出函数![]() 在区间
在区间![]() 上的图像.
上的图像.
10.函数![]() 的单调递减区间是
.
的单调递减区间是
.
【巩固练习】
一、选择题:
1.下列不等式中正确的是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.若![]() ,则函数
,则函数![]() 的
( )
的
( )
(A)最小值为0,无最大值 (B)最小为0,最大值为6
(C)最小值为![]() ,无最大值 (D)最小值为
,无最大值 (D)最小值为![]() ,最大值为6
,最大值为6
3.已知奇函数![]() 在[-1,0]上为单调递增函数,且
在[-1,0]上为单调递增函数,且![]() 、
、![]() 为锐角三角形的内角,则( )
为锐角三角形的内角,则( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
4.在①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 这四个函数中,最小正周期为
这四个函数中,最小正周期为![]() 的函数序号为 ( )
的函数序号为 ( )
(A)①②③ (B)①④ (C)②③ (D)以上都不对
5.给出如下四个函数①![]() ②
②![]() ③
③![]()
④![]() 其中奇函数的个数是 ( )
其中奇函数的个数是 ( )
(A)1个 (B)2个 (C)3个 (D)4个
 6.函数
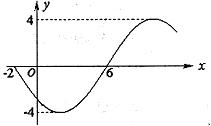
6.函数![]() 的部分图象如图所示,则函数表达式为
的部分图象如图所示,则函数表达式为
( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.在△ABC中,![]() ,则△ABC的形状为 ( )
,则△ABC的形状为 ( )
(A)等腰三角形 (B)直角三角形 (C)等腰直角三角形 (D)等腰三角形或直角三角形
8.设![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
二、填空题:
9. α是第二象限角,P(x,![]() )为其终边上一点,且
)为其终边上一点,且![]() ,则
,则![]() 的值为
.
的值为
.
10. 已知![]() ,则
,则![]() 的值是 .
的值是 .
11. 已知![]() ,则
,则![]() .
.
12. 设函数![]() ,若
,若![]() 是偶函数,则
是偶函数,则![]() 的最小正值是 .
的最小正值是 .
13. 函数y=sinx+acosx的一条对称轴的方程是x=![]() ,则直线ax+y+1=0的倾斜角为
.
,则直线ax+y+1=0的倾斜角为
.
三、解答题:
14.设q ∈(0,p),sinq+cosq=![]() .
.
(1)求sin4q+cos4q的值;
(2)求cos2q的值.
15.若![]() 试求:
试求:
(1)![]() 的值
的值
(2)![]() 的值
的值
16.已知函数 f (x) = sin (2x+![]() ) + sin (2x-
) + sin (2x-![]() )+cos2x+a (a∈R) .
)+cos2x+a (a∈R) .
(1)求函数的最小正周期;
(2)求函数的单调递减区间;
(3)若x∈[0,![]() ]时,f(x)的最小值为-2,求a的值.
]时,f(x)的最小值为-2,求a的值.
17.设关于![]() 的函数
的函数![]() 的最小值为
的最小值为![]() .
.
(1)写出![]() 的表达式;
的表达式;
(2)试确定能使![]() 的
的![]() 值,并求出此时函数
值,并求出此时函数![]() 的最大值.
的最大值.
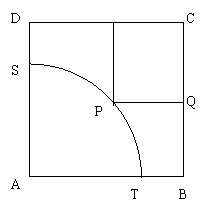
18.如图,ABCD是一块边长为100m的正方形地皮,其中AST是一半径为90m的扇形小山,其余部分都是平地。一开发商想在平地上建一个矩形停车场,使矩形的一个顶点在弧ST上,相邻两边CQ、CR落在正方形的边BC、CD上,求矩形停车场PQCR面积的最大值。
 |
高一数学复习——三角函数
班级 姓名
【复习要点】
4. 了解任意角的概念和弧度制;借助单位圆理解掌握三角函数的定义;理解同角三角函数的基本关系;熟练运用诱导公式。
5. 结合三角函数图象理解三角函数的性质(周期性,单调性,最大和最小值等)
6. 结合![]() 的图象观察参数的变化对函数图象的影响;能应用三角函数解决一些简单的实际问题。
的图象观察参数的变化对函数图象的影响;能应用三角函数解决一些简单的实际问题。
【例题分析】
1.已知2弧度的圆心角所对的弧长为![]() ,则此圆心角所对的扇形面积是___
,则此圆心角所对的扇形面积是___![]() ____.
____.
2.方程![]() 的实根个数为 3个 .
的实根个数为 3个 .
3.函数![]() 的定义域是
的定义域是![]()
4.要得到![]() 的图象只
的图象只![]() 的图象 ( D )
的图象 ( D )
A. 右移 B. 左移 C. 右移 D. 左移
5.已知![]() 的值是 3 .
的值是 3 .
6.已知![]() .
.
(I)求sinx-cosx的值;
(Ⅱ)求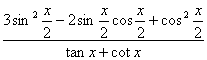 的值.
的值.
解法一:(Ⅰ)由![]()
即 ![]()
又![]() 故
故 ![]()
(Ⅱ)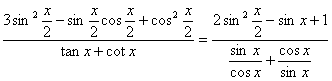
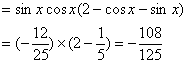
|
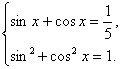
由①得![]() 将其代入②,整理得
将其代入②,整理得![]()
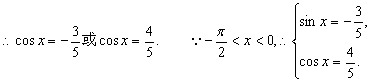 故
故 ![]()
(Ⅱ)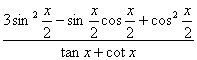
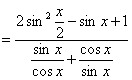
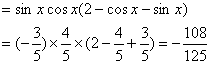
7.化简![]() 并求函数
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
解:
![]()
![]()
![]()
所以函数f(x)的值域为![]() ,最小正周期
,最小正周期![]()
8.函数![]() 的最小正周期是
的最小正周期是 ![]() .
.
9.设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() 。
。
(Ⅰ)求![]() ; (Ⅱ)求函数
; (Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)画出函数![]() 在区间
在区间![]() 上的图像.
上的图像.
解:(Ⅰ)![]() 的图像的对称轴,
的图像的对称轴,![]()
![]()
![]()
(Ⅱ)由(Ⅰ)知![]()
由题意得 ![]()
所以函数![]()
(Ⅲ)由![]()
| x | 0 |
|
|
|
|
|
| y |
| -1 | 0 | 1 | 0 |
|
|
10.函数![]() 的单调递减区间是
的单调递减区间是 ![]() .
.
【巩固练习】
四、选择题:
1.下列不等式中正确的是 ( BD )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2. 若![]() ,则函数
,则函数![]() 的
( B
)
的
( B
)
(A)最小值为0,无最大值 (B)最小为0,最大值为6
(C)最小值为![]() ,无最大值 (D)最小值为
,无最大值 (D)最小值为![]() ,最大值为6
,最大值为6
3.已知奇函数![]() 在[-1,0]上为单调递增函数,且
在[-1,0]上为单调递增函数,且![]() 、
、![]() 为锐角三角形的内角,则
为锐角三角形的内角,则
( C )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
4.在①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 这四个函数中,最小正周期为
这四个函数中,最小正周期为![]() 的函数序号为 ( C
)
的函数序号为 ( C
)
(A)①②③ (B)①④ (C)②③ (D)以上都不对
5.给出如下四个函数①![]() ②
②![]() ③
③![]()
④![]() 其中奇函数的个数是 ( A )
其中奇函数的个数是 ( A )
(A)1个 (B)2个 (C)3个 (D)4个
 6.函数
6.函数![]() 的部分图象如图所示,则函数表达式为
的部分图象如图所示,则函数表达式为
( A )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.在△ABC中,![]() ,则△ABC的形状为 ( D
)
,则△ABC的形状为 ( D
)
(A)等腰三角形 (B)直角三角形 (C)等腰直角三角形 (D)等腰三角形或直角三角形
8.设![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的取值范围是 ( B
)
的取值范围是 ( B
)
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
五、填空题:
9. α是第二象限角,P(x,![]() )为其终边上一点,且
)为其终边上一点,且![]() ,则
,则![]() 的值为
的值为![]() .
.
10. 已知![]() ,则
,则![]() 的值是
的值是 ![]() .
.
11. 已知![]() ,则
,则![]()
![]() .
.
12. 设函数![]() ,若
,若![]() 是偶函数,则
是偶函数,则![]() 的最小正值是
的最小正值是 ![]() .
.
13. 函数y=sinx+acosx的一条对称轴的方程是x=![]() ,则直线ax+y+1=0的倾斜角为
,则直线ax+y+1=0的倾斜角为![]() .
.
六、解答题:
14.设q ∈(0,p),sinq+cosq=![]() .
.
(1)求sin4q+cos4q的值;
(2)求cos2q的值.
(1)![]() (2)-
(2)-![]()
15. 若![]() 试求:
试求:
(1)![]() 的值
的值
(2)![]() 的值
的值
![]()
16.已知函数 f (x) = sin (2x+![]() ) + sin (2x-
) + sin (2x-![]() )+cos2x+a (a∈R) .
)+cos2x+a (a∈R) .
(1)求函数的最小正周期;
(2)求函数的单调递减区间;
(3)若x∈[0,![]() ]时,f(x)的最小值为-2,求a的值.
]时,f(x)的最小值为-2,求a的值.
(1)T=π (2)[kπ+![]() , kπ+
, kπ+![]() ] (k∈Z) (3)a=-1
] (k∈Z) (3)a=-1
17.设关于![]() 的函数
的函数![]() 的最小值为
的最小值为![]() .
.
(3)写出![]() 的表达式;
的表达式;
(4)试确定能使![]() 的
的![]() 值,并求出此时函数
值,并求出此时函数![]() 的最大值.
的最大值.
(1) f(a)=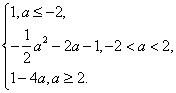
(2) a=-1, ymax=5
18.如图,ABCD是一块边长为100m的正方形地皮,其中AST是一半径为90m的扇形小山,其余部分都是平地。一开发商想在平地上建一个矩形停车场,使矩形的一个顶点在弧ST上,相邻两边CQ、CR落在正方形的边BC、CD上,求矩形停车场PQCR面积的最大值。
 |
![]()