高一数学复习——三角恒等变换
班级 姓名
一、复习要点:
1.熟记以下公式:
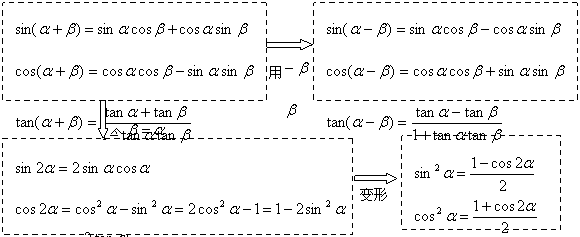 |
你能在空白纸上独立地默写一遍吗?你还记得万能代换公式和其他常用结论吗?与你的同桌比一比,看谁写得多?
2.三角变换主要有变名、变角与变形三种,如利用两角和与差的三角函数、二倍角公式、降幂公式等。
3.不仅要熟练掌握基本公式,更要做到思路开阔,善于选择适当的公式进行变换。对于有条件的求值、化简、证明问题,关键是找出条件与结论之间角、函数名称等之间的差异及联系。
二、例题分析
1.![]() 中,
中,![]() ,试判断
,试判断![]() 的形状。
的形状。
2.若![]() ,求
,求![]() 。
。
3.化简![]() 。
。
4.已知![]() ,
,![]() ,求
,求![]() 。
。
5.已知![]() 为锐角,且
为锐角,且![]() ,
,![]() ,求
,求![]() 的值。
的值。
6.已知![]() 为锐角,
为锐角,![]() ,
,![]() ,求证:
,求证:![]() 成等差数列。
成等差数列。
7.已知![]() ,其中
,其中![]() 为锐角,求
为锐角,求![]() 的最大值。
的最大值。
8.求关于x的函数![]() (
(![]() )的最大值与最小值。
)的最大值与最小值。
9.已知函数![]() ,求:
,求:
(1)![]() 的最大值
的最大值![]() ;(2)求
;(2)求![]() 的最小值。
的最小值。
三、巩固练习
1.锐角三角形ABC中,有 ( )
(A)sinA>cosB (B)sinA>sinB (C)sinA<cosB (D)sinA<sinB
2.若![]() ,则
,则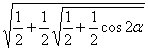 等于 ( )
等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.函数![]() 的最小正周期是 ( )
的最小正周期是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.![]() 、
、![]() 均为锐角,
均为锐角,![]() ,
,![]() ,则
,则![]() 、
、![]() 的关系是 ( )
的关系是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.函数![]() 的最小正周期是
。
的最小正周期是
。
6.函数![]() 在
在![]() 上的值域是
。
上的值域是
。
7.函数![]() 的最大值是
。
的最大值是
。
8.化简![]() =
。
=
。
9.已知函数![]() 为偶函数,求
为偶函数,求![]() 的值。
的值。
10.已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值。
的值。
11.△ABC中,![]() ,求函数
,求函数![]() 的值域。
的值域。
12.求函数![]() 的最大值
的最大值![]() ,并求
,并求![]() 的最小值。
的最小值。
题量及运算量较大,建议选用。
以下答案仅供参考:
例1.等腰三角形
例2.![]()
例3.![]()
例4.![]()
例5.![]()
例6.考察![]() ,把
,把![]() 代入
代入
例7.![]()
例8.当![]() 时。
时。![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]()
例9.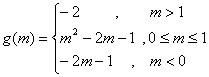 ,
,![]()
巩固练习:
1.A
2.C
3.B
4.C
5.![]()
6.![]()
7.1
8.![]()
9.![]()
10.![]()
11.![]()
12.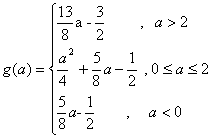 ,无最小值
,无最小值