高一数学数列与等差数列试题

高一数学同步测试（11）—数列与等差数列

一、选择题：

1．有穷数列1， 2³， 2⁶， 2⁹， …，2^3n＋6的项数是　　　　　　　　　　 　　　　　　　　　　　　 （　　）

　　A．3n＋7　　　　　　 B．3n＋6　　　　 　C．n＋3　　 　　　　　D．n＋2

2．已知数列的首项，且，则为　　 　　　　　　　 （　　）

A．7　　　　　  　　B．15　　　　  　　C．30　　　　　 　　D．31

3．某数列第一项为1，并且对所有n≥2，n∈N^*，数列的前n项之积n²，则这个数列的通项公式是　　　　　　　　　　（　　）

A．a_n=2n－1　　　　　　　　　　　　　　　　　　　　　　B．a_n=n²

C．a_n=　　　　　　　　　　　　　　　　　　　　D．a_n=

4．若{a_n}是等差数列，且a₁＋a₄＋a₇=45，a₂＋a₅＋a₈=39，则a₃＋a₆＋a₉的值是　　（　　）

A．39　　　　　　　　　　　B．20　　　　　　　　　　　 C．19.5　　　　　　　　　　D．33

5．若等差数列{a_n}的前三项为x－1，x＋1，2x＋3，则这数列的通项公式为　　　　　 （　　）

A．a_n=2n－5　　　　　　B． a_n =2n－3　　　　　C． a_n =2n－1　　　　 D．a_n =2n＋1

6．首项为－24的等差数列，从第10项起开始为正数，则公差的取值范围是　　　　　（　　）

A．d＞　　　　　　　　 B．d＜3　　　　　　　　　 C．≤d＜3　　　　　　D． ＜d≤3

7．等差数列{a_n}的前n项和S_n=2n²＋n，那么它的通项公式是　　　　　　　　　　　　　　　　 （　　）

A．a_n =2n－1　　　　　　B．a_n =2n＋1　　　　　 C．a_n =4n－1　　　　　 D．a_n =4n＋1

8．中，则值最小的项是　　　　　　　　　　　  　　　　　（　　）

A．第4项　　　　　 　　　　　　　　　　　　　　　 B．第5项　　　 　　

C．第6项　　　　　 　　　　　　　　　　　　　　　 D．第4项或第5项

9．已知，则的值为　　　　  　　　　　（　　）

　　　A．　　　　　　 B．　　  　C．　　　 　D．

10．在等差数列{a_n}中，若a₃＋a₉＋a₁₅＋a₂₁=8，则a₁₂等于　　　　　 　　　　　　　　　　　　 （　　）

A．1　　　　　　　　　　　　B．－1　　　　　　　　　　 C．2　　　　　　　　　　　　D．－2

11．在等差数列{a_n}中，a₃＋a₇－a₁₀=8，a₁－a₄=4，则S₁₃等于　　　 　　　　　　　　　　　　 （　　）

A．168　　　　　　　　　　 B．156　　　　　　　　　　 C．78　　　　　　　　　　　D．152

12．数列{a_n}的通项a_n =2n＋1，则由b_n=(n∈N^*)，所确定的数列{b_n}的前n项和是　　　 　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．n(n＋1)　　　　　　　 B．　　　　　　C．　　　　　　 D．

二、填空题：

13．数列1，0，－1，0，1，0，－1，0，…的通项公式的为a_n=　　　　　　　　　　　  ．

14．在－1，7之间插入三个数，使它们顺次成等差数列，则这三个数分别是_　　　　______．

15．数列{ a_n }为等差数列，a₂与a₆的等差中项为5，a₃与a₇的等差中项为7，则数列的通项a_n等于__　　　　　　　　　  _.

16、数列{a_n}为等差数列，S₁₀₀=145，d=，则a₁＋a₃＋a₅＋…＋a₉₉的值为___　　　　　__．

三、解答题：

17．已知关于x的方程x²－3x＋a=0和x²－3x＋b=0(a≠b)的四个根组成首项为的等差数列，求a＋b的值.

 

18．在数列{a_n}中，a₁=2，a₁₇=66，通项公式是项数n的一次函数.

(1)求数列{a_n}的通项公式；　

(2)88是否是数列{a_n}中的项.

19．数列｛a_n｝是首项为23，公差为整数的等差数列，且第六项为正，第七项为负.

（1）求数列的公差；

（2）求前n项和S_n的最大值；

（3）当S_n＞0时，求n的最大值．

 

20．设函数，数列的通项满足．

（1）求数列的通项公式；

（2）判定数列{a _n }的单调性.

 

21．已知数列{a_n}满足a₁=4，a_n=4－ (n≥2)，令b_n=．

（1）求证数列{b_n}是等差数列；

（2）求数列{a_n}的通项公式.

 

22．某公司决定给员工增加工资，提出了两个方案，让每位员工自由选择其中一种.甲方案是：公司在每年年末给每位员工增资1000元；乙方案是每半年末给每位员工增资300元.某员工分别依两种方案计算增资总额后得到下表：

工作年限	方案甲	方案乙	最终选择
1	1000	600	方案甲
2	2000	1200	方案乙
≥3			方案甲

(说明：①方案的选择应以让自己获得更多增资为准. ②假定员工工作年限均为整数.)

（1）他这样计算增资总额，结果对吗？如果让你选择，你会怎样选择增资方案？说明你的理由；

（2）若保持方案甲不变，而方案乙中每半年末的增资数改为a元，问：a为何值时，方案乙总比方案甲多增资？

 

参考答案

一、选择题： CDCDB　DCDBC　BC

二、填空题： 13.sin或a_n =．14.1，3，5．15.2n－3．16、60．

三、解答题：

17.解析：由方程x²－3x＋a=0和x²－3x＋b=0(a≠b)可设两方程的根分别为x₁，x₂和x₃，x₄，

由x₁＋x₂=3和x₃＋x₄=3

所以，x₁，x₃，x₄，x₂(或x₃，x₁，x₂，x₄)组成等差数列，

由首项x₁=，x₁＋x₃＋x₄＋x₂=6，可求公差d=，

所以四项为：，

∴a＋b=．

18.解析： (1)设a_n=An＋B，由a₁=2，a₁₇=66，得

∴a_n=4n－2

(2)令a_n=88，即4n－2=88得n=N*

∴88不是数列{a_n}中的项.

19.解析： (1)由已知a₆=a₁＋5d=23＋5d＞0，a₇=a₁＋6d=23＋6d＜0，

解得:－＜d＜－，又d∈Z，∴d=－4

(2)∵d＜0，∴{a_n}是递减数列，又a₆＞0，a₇＜0

∴当n=6时，S_n取得最大值，S₆=6×23＋ (－4)=78

(3)S_n=23n＋ (－4)＞0，整理得：n(50－4n)＞0

∴0＜n＜，又n∈N*，

所求n的最大值为12.

20.解析：⑴∵，又，

∴

令，则，∴，

注意到，因此＝， ，

，　　∴即为数列的通项公式；

另解：由已知得

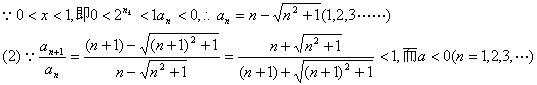
，可知数列是递增数列.

注：数列是一类特殊的函数，判定数列的单调性与判定函数的单调性的方法是相同的，只需比较a_n＋1与a_n的大小．

21.(1)证明： a_n＋1－2=2－

∴ (n≥1)

故(n≥1)，即b_n＋1－b_n= (n≥1)

∴数列{b_n}是等差数列.

(2)解析： ∵{}是等差数列

∴，　 ∴a_n=2＋

∴数列{a_n}的通项公式a_n=2＋

22.解析： (1)设根据甲方案第n次的增资额为a_n，则a_n=1000n

第n年末的增资总额为T_n=500n(n＋1)

根据乙方案，第n次的增资额为b_n，则b_n=300n

第n年末的增资总额为S_2n=300n(2n＋1)

∴T₁=1000，S₂=900，T₁＞S₂只工作一年选择甲方案T₂=3000，S₄=3000，T₂=S₄

当n≥3时，T_n＜S_2n，因此工作两年或两年以上选择乙方案.

(2)要使T_n=500n(n＋1)，S_2n=an(2n＋1)

S_2n＞T_n对一切n∈N*都成立即a＞500·

可知{500}为递减数列，当n=1时取到最大值.

则a＞500·= (元)，即当a＞时，方案乙总比方案甲多增资.