高一数学同步测试（13）—数列单元测试题
一、选择题
1．若Sn是数列{an}的前n项和，且
则
是 （ ）
A．等比数列，但不是等差数列 B．等差数列，但不是等比数列
C．等差数列，而且也是等比数列 D．既非等比数列又非等差数列
2．某种细菌在培养过程中，每20分钟分裂一次(一个分裂为两个)，经过3小时，这种细菌由1个可繁殖成 （ ）
A．511个 B．512个 C．1023个 D．1024个
3．等差数列{a
n}中，已知
（ ）
A．48 B．49 C．50 D．51
4．已知{an}是等比数列，且an＞0，a2a4＋2a3a5＋a4a6=25，那么a3＋a5的值等于 （ ）
A．5 B．10 C．15 D．20
5．等比数列｛an｝的首项a1＝1，公比q≠1，如果a1，a2，a3依次是某等差数列的第1，2，5项，则q等于 （ ）
A．2 B．3 C．－3 D．3或－3
6．等比数列｛an｝的前3项的和等于首项的3倍，则该等比数列的公比为 （ ）
A．－2 B．1 C．－2或1 D．2或－1
7．已知方程
的四个根组成的一个首项为
的等差数列，则
（ ）
A．1 B．
C．
D．
8．数列{an}中，已知S1 =1， S2=2 ，且Sn＋1－3Sn ＋2Sn－1 =0(n∈N*)，则此数列为（ ）
A．等差数列 B．等比数列
C．从第二项起为等差数列 D．从第二项起为等比数列
9．等比数列前
项和为54，前
项和为60，则前
项和为
（ ）
A．66
B．64
C．
D．
10．设等差数列{an}的公差为d，若它的前n项和Sn=－n2，则 （ ）
A．an=2n－1，d=－2 B．an=2n－1，d=2
C．an=－2n＋1，d=－2 D．an=－2n＋1，d=2
11．数列{an}的通项公式是a n =
(n∈N*)，若前n项的和为10，则项数为（ ）
A．11 B．99 C．120 D．121
12．某人于2000年7月1日去银行存款a元，存的是一年定期储蓄，计划2001年7月1日将到期存款的本息一起取出再加a元之后还存一年定期储蓄，此后每年的7月1日他都按照同样的方法在银行取款和存款．设银行一年定期储蓄的年利率r不变，则到2005年7月1日他将所有的存款和本息全部取出时，取出的钱共为 （ ）
A．a(1＋r)4元 B．a(1＋r)5元
C．a(1＋r)6元 D．
［(1＋r)6－(1＋r)］元
二、填空题：
13．设｛an｝是公比为q的等比数列，Sn是它的前n项和，若｛Sn｝是等差数列，
则q= ．
14．设数列
满足
，
当
时，
．
15．数列的前ｎ项的和Sn =3n2＋ n＋1，则此数列的通项公式a n=__
．
16．在等差数列
中，当
时，必定是常数数列．然而在等比数列 中，对某些正整数
、
，当时，非常数数列的一个例子是
___
___．
三、解答题：
17．已知：等差数列{
}中，
=14，前10项和
．
（1）求；
（2）将{}中的第2项，第4项，…，第
项按原来的顺序排成一个新数列，求此数列的前项和
．
18．求下面各数列的和：
（1）
；
（2）
19．数列｛an｝满足a1=1，an=
an－1＋1(n≥2)
（1）若bn=an－2，求证｛bn｝为等比数列；
（2）求｛an｝的通项公式．
20．某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用12万元，以后每年都增加4万元，每年捕鱼收益50万元，
（1）问第几年开始获利？
（2）若干年后，有两种处理方案：
（3）年平均获利最大时，以26万元出售该渔船；
（4）总纯收入获利最大时，以8万元出售该渔船．
问哪种方案合算．
21．已知数列是等差数列，且
（1）求数列的通项公式；
（2）令
求数列
前n项和的公式．
22．某房地产公司推出的售房有两套方案：一种是分期付款的方案，当年要求买房户首付3万元，然后从第二年起连续十年，每年付款8000元；另一种方案是一次性付款，优惠价为9万元，若一买房户有现金9万元可以用于购房，又考虑到另有一项投资年收益率为5%，他该采用哪种方案购房更合算？请说明理由．(参考数据1.059≈1.551，1.0510≈1.628)
参考答案
一、选择题：BBCAB CCDDC CD
二、填空题：13.１．14.
．
15.
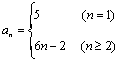．16、
，
与
同为奇数或偶数．
三、解答题：
17．解析：(1)由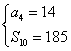
∴ 
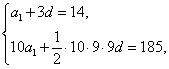
由
(1)设新数列为{
}，由已知，
18.解析：(1)
(本题用到的方法称为“裂项法”，把通项公式化为an=f(n＋1)－f(n)的形式)
(2)通项
呈“等差×等比”的形式，
19.解析： (1)由an=an－1＋1得an－2= (an－1－2)
即
，(n≥2)
∴｛bn｝为以－1为首项，公比为的等比数列
(2)bn=(－1)( )n－1，即an－2=－()n－1
∴an=2－()n－1
20.解析：（1）由题设知每年费用是以12为首项，4为公差的等差数列，设纯收入与年数的关系为
，
∴
，
获利即为＞0， ∴
，
解之得：
，
又n∈N， ∴n=3，4，…，17， ∴当n=3时即第3年开始获利；
（1）(i)年平均收入=
∵
≥
，当且仅当n=7时取“=”，
∴
≤40－2×14=12(万元)即年平均收益，总收益为12×7＋26=110万元，此时n=7．
(ii)
，∴当
总收益为102＋8=110万元，此时n=10，比较两种方案，总收益均为110万元，但第一种方案需7年，第二种方案需10年，故选择第一种．
21．解析：设数列公差为
，则 
又
所以
(Ⅱ)解：令
则由
得
① 
②
当
时，①式减去②式，得 
所以
当
时， 
，综上可得当时，
当时，
22．解析：如果分期付款，到第十一年付清后看其是否有结余，设首次付款后第n年的结余数为an，
∵a1=(9－3)×(1＋0.5%)－0.8=6×1.05－0.8
a2=(6×1.05－0.8)×1.05－0.8=6×1.052－0.8×(1＋1.05)
……
a10=6×1.0510－0.8(1＋1.05＋…＋1.059)
=6×1.0510－0.8×
=6×1.0510－16×(1.0510－1)
=16－10×1.0510
≈16－16.28=－0.28(万元)
所以一次性付款合算．