概率的应用练习
1、某厂的三个车间的职工代表在会议室开会,第一、二、三车间的与会人数分别是
10、12、9，一个门外经过的工人听到发言，则发言人是第二或第三车间职工代
表的概率是 （ ）
A．
B. 
C
D.
2、从1，2，3，4这4个数中，不放回地任意取两个数，两个数都是偶数的概率是
（A）
（B）
（C）
（D）
3、随机事件A的频率
满足( )
A. 
B. 
C. 
D. 
4、从分别写有A、B、C、D、E的5张卡片中,任取2张,这2张中的字母恰好按字母
顺序相邻的概率( )
A.
B. 
C.
D.
5、从装有3个白球,2个黑球的盒子中任取两球,则取到全是白球的概率是( )
A.
B. C.
D.
6、一栋楼房有4个单元,甲、乙两人都在此楼内,甲、乙同住一单元的概率( )
A.
B. 
C.
D.
7、甲、乙2人下棋，下成和棋的概率是，乙获胜的概率是
，则甲不胜的概率是（ ）
A．
B．
C． D．
8、从装有两个红球和两个黑球的口袋里任取两个球，那么互斥而不对立的两个事件是（ ）
A．“至少有一个黑球”与“都是黑球”
B．“至少有一个黑球”与“至少有一个红球”
C．“恰好有一个黑球”与“恰好有两个黑球”
D．“至少有一个黑球”与“都是红球”
9、一枚硬币连抛3次，只有一次出现正面的概率是（ ）
A．
B． C．
D．
10、某小组共有10名学生，其中女生3名，现选举2名代表，至少有1名女生当
选的概率为（ ）
A．
B．
C．
D．
11、从4台甲型和5台乙型电视机中任意取出3台，则至少要有甲型与乙型电视机各
一台的概率是（ ）
A．
B．1
C． D．
12、取一根长度为3m的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不小于
1m的概率是（ ）
A．
B．
C．
D．不确定
13、在1万
的海域中有40的大陆架储藏着石油，假如在海域中任意一点钻探，
钻到油层的概率是（ ）
A．
B．
C．
D．
14、随意安排甲、乙、丙3人在节日中值班，每人值班一天，则甲排在乙前的概率为
15、袋中有大小相同的红、黄两种颜色的球各1个，从中任取1只，有放回地抽取3次．求：
（Ⅰ）3只全是红球的概率；
（Ⅱ）3只颜色全相同的概率；
（Ⅲ）3只颜色不全相同的概率．
16、一盒中装有20个大小相同的弹子球，其中红球10个，白球6个，黄球 4个，
一小孩随手拿出4个，求至少有3个红球的概率
17、在长度为10的线段内任取两点将线段分为三段，求这三段可以构成三角形的概率
18、（镇江）某班数学兴趣小组有男生和女生各３名，现从中任选２名学生去参加校
数学竞赛，求：
（I）恰有一名参赛学生是男生的概率；
（II）至少有一名参赛学生是男生的概率；
（Ⅲ）至多有一名参赛学生是男生的概率。
概率的应用练习答案
1、D 2、A 3、D 4、B 5、A 6、A 7、B 8、C 9、A 10、B 11、C
12、B 13、C 14、
15、解：由于是有放回地取球，因此袋中每只球每次被取到的概率均为
．……3分
（Ⅰ）3只全是红球的概率为P1＝··＝
．
……6分
（Ⅱ）3只颜色全相同的概率为P2＝2·P1＝2·＝
．
……9分
（Ⅲ）3只颜色不全相同的概率为P3＝1－P2＝1－＝
．
……12分
16、解：恰有3个红球的概率P1= 
4′有4个红球的概率P2=
8′
至少有3个红球的概率P=P1+P2=
…………12
17、解：设构成三角形的事件为A，长度为10的线段被分成三段的长度分别为x，y，
10－（x＋y）， ……2分
则 
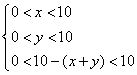，即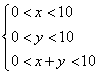
…4由一个三角形两边之和大于第三边，有
，即
．
……6分
又由三角形两边之差小于第三边，有
，即
，同理
．
∴ 构造三角形的条件为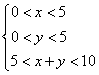
．
……8分
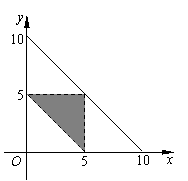
∴ 满足条件的点P（x，y）组成的图形是如图所示中的阴影区域（不包括区域的边界）．
，
．∴ 
……10分
18．基本事件的种数为
=15种 （Ⅰ）恰有一名参赛学生是男生的基本事件有
=9种 
这一事件的概率P1=
=0.6（5分）（Ⅱ）至少有一名参赛学生是男生这一事件是由两类事件构成的，即恰有一名参赛学生是男生和两名参赛学生都是男生所求事件的概率P2=
（9分）（Ⅲ）同理至多有一名参赛学生是男生的概率