（数学3必修）第三章 概率
[综合训练B组]
一、选择题
1
同时向上抛
个铜板，落地时个铜板朝上的面都相同，你认为对这个铜板下面情况更可能正确的是（ ）
Ａ 这个铜板两面是一样的
Ｂ 这个铜板两面是不同的
Ｃ 这个铜板中有
个两面是一样的，另外个两面是不相同的
Ｄ 这个铜板中有
个两面是一样的，另外
个两面是不相同的
2 口袋内装有一些大小相同的红球、白球和黒球，从中摸出
个球，摸出红球的概率是
，摸出白球的概率是
，那么摸出黒球的概率是（ ）
A B C 
D 
3 从装有
个红球和个黒球的口袋内任取个球，那么互斥而不对立的两个事件是（ ）
A 至少有一个黒球与都是黒球
B 至少有一个黒球与都是黒球
C 至少有一个黒球与至少有个红球 D 恰有个黒球与恰有个黒球
4 在
根纤维中，有
根的长度超过
，从中任取一根，取到长度超过的纤维的概率是（ ）
A 
B 
C 
D 以上都不对
5 先后抛掷骰子三次，则至少一次正面朝上的概率是（ ）
A 
B 
C 
D 
6 设
为两个事件，且
，则当（ ）时一定有
A 
与
互斥 B 与对立 Ｃ 
Ｄ 不包含
二、填空题
1 在
件产品中，
有件一级品，
件二级品，则下列事件：
①在这件产品中任意选出
件，全部是一级品；
②在这件产品中任意选出件，全部是二级品；
③在这件产品中任意选出件，不全是一级品；
④在这件产品中任意选出件，其中不是一级品的件数小于，
其中 是必然事件； 是不可能事件； 是随机事件
2 投掷红、蓝两颗均匀的骰子，观察出现的点数，至多一颗骰子出现偶数点的概率是_____
3 在区间
中随机地取出两个数，则两数之和小于
的概率是______________
4 在
的水中有一个草履虫，现从中随机取出
水样放到显微镜下观察，则发现草履虫的概率是_____________
三、解答题
1 袋中有大小相同的红、黄两种颜色的球各个，从中任取只，有放回地抽取
次 求：
① 只全是红球的概率；
② 只颜色全相同的概率；
③ 只颜色不全相同的概率
2 抛掷颗质地均匀的骰子，求点数和为的概率
3 从
名男生和名女生中任选人参加演讲比赛,
①求所选人都是男生的概率;
②求所选人恰有名女生的概率;
③求所选人中至少有名女生的概率
4 平面上画了一些彼此相距
的平行线，把一枚半径
的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率
数学3（必修） 第三章 概率 [综合训练B组]
参考答案
一、选择题
1 A
假设正反两面是不同的，则相同的面次都朝上的概率为
这个概率太小了，几乎是不可能事件
2 C
3 D 4 B 在根纤维中，有根的长度超过，即基本事件总数为，且它们是等可能发生的，所求事件包含个基本事件，故所求事件的概率为
5 D
至少一次正面朝上的对立事件的概率为
6 B
对立事件
二、填空题
1 ③,④; ②; ①
2 
其对立事件为都出现奇数点，
3 
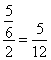4 
三、解答题
1 解：①每次抽到红球的概率为
②每次抽到红球或黄球
③颜色不全相同是全相同的对立，
2 解：在抛掷颗骰子的试验中，每颗骰子均可出现点，点，…，
点种不同的结果，我们把两颗骰子标上记号
以便区分，因此同时掷两颗骰子的结果共有
，在上面的所有结果中，向上的点数之和为的结果有
，共
种，所以，所求事件的概率为
3 解：基本事件的总数为
①所选人都是男生的事件数为
②所选人恰有女生的事件数为
③所选人恰有女生的事件数为
所选人中至少有名女生的概率为
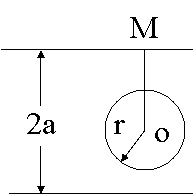
4 解：把“硬币不与任一条平行线相碰”的事件记为事件，为了确定硬币的位置，由硬币中心
向靠得最近的平行线引垂线
，垂足为
，如图所示，这样线段长度（记作）的取值范围就是
，只有当
时硬币不与平行线相碰，所以所求事件的概率就是
=