高一数学点直线平面之间的位置关系测试题

高一数学点直线平面之间的位置关系测试题

（时间：60分钟，满分：100分）

班别　　　　　  座号　　　　　 姓名　　　　　　　　 成绩　　　　　　　　

一、选择题（本大题共10小题，每小题5分，共50分）

1.若直线a不平行于平面，则下列结论成立的是（　　　）

A. 内所有的直线都与a异面；　　  B. 内不存在与a平行的直线；

C. 内所有的直线都与a相交；　　  D.直线a与平面有公共点.

2.已知两个平面垂直，下列命题

①一个平面内的已知直线必垂直于另一个平面的任意一条直线；

②一个平面内的已知直线必垂直于另一个平面的无数条直线；

③一个平面内的任一条直线必垂直于另一个平面；

④过一个平面内任意一点作交线的垂线，则垂线必垂直于另一个平面.

其中正确的个数是（　　 ）　A.3　　 B.2　　　C.1　　 D.0

3.空间四边形ABCD中，若，则与所成角为

A、　　B、　　 C、　　D、

4. 给出下列命题：

（1）直线a与平面不平行，则a与平面内的所有直线都不平行；

（2）直线a与平面不垂直，则a与平面内的所有直线都不垂直；

（3）异面直线a、b不垂直，则过a的任何平面与b都不垂直；

（4）若直线a和b共面，直线b和c共面，则a和c共面

其中错误命题的个数为（　 ）　（A）0　 （B） 1　　（C）2　 （D）3

5．正方体ABCD-A₁B₁C₁D₁中，与对角线AC₁异面的棱有（　 ）条　A 3　 B 4　 C 6　 D 8

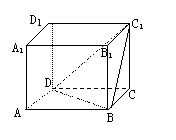6. 点P为ΔABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，则点O是ΔABC的（　 ）　 （A）内心　（B）外心　 （C）重心　 （D）垂心

7.如图长方体中，AB=AD=2，CC₁=，则二面角

　C₁—BD—C的大小为（　　）

 （A）30⁰　　（B）45⁰　 （C）60⁰　（D）90⁰

8.直线a,b,c及平面α,β,γ,下列命题正确的是（　　）

A、若aα，bα,c⊥a, c⊥b 则c⊥α　　 B、若bα, a//b　则 a//α　

C、若a//α,α∩β=b  则a//b　　　 D、若a⊥α, b⊥α 则a//b

9.平面与平面平行的条件可以是（　　　 ）

A.内有无穷多条直线与平行；　　　　 B.直线a//,a//

C.直线a,直线b,且a//,b//　　  D.内的任何直线都与平行

10、 a, b是异面直线，下面四个命题：

①过a至少有一个平面平行于b； ②过a至少有一个平面垂直于b；

③至多有一条直线与a，b都垂直；④至少有一个平面与a，b都平行。

其中正确命题的个数是（　　　　）Ａ　０　　Ｂ　１　　Ｃ　２　　Ｄ　３

选择题答题表

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题（本大题共4小题，每小题5分，共20分）

11.已知直线a//平面，平面//平面，则a与的位置关系为　　　　　　　　  .

12．已知直线a⊥直线b, a//平面,则b与的位置关系为　　　　　　　　   .

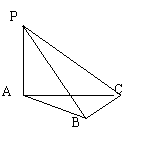13如图，ABC是直角三角形，ACB=，PA平面ABC，此图形中有　 个直角三角形

14.α、β是两个不同的平面，m、n是平面α及β之外的两条不同直线,

给出四个论断：

① m ^ n　 ②α^β ③ m ^β ④ n ^α

以其中三个论断作为条件，余下一个论断作为结论，写出你认为

正确的一个命题：______________________________________.

三、解答题（本大题共3小题，每小题10分，共30分）

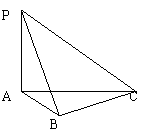15．如图，PA⊥平面ABC，平面PAB⊥　　 16．在三棱锥S-ABC中，已知AB=AC，平面PBC　 求证：AB⊥BC　　　　 　　　　　　　O是BC的中点，平面SAO⊥平面ABC

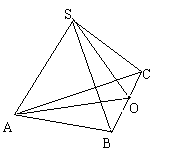求证：∠SAB=∠SAC

　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　

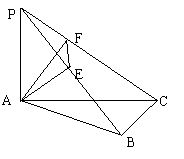
17．如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC,PA=AB=BC=2（1）求证：平面AEF⊥平面PBC；

（2）求二面角P—BC—A的大小；（3）求三棱锥P—AEF的体积.

参考答案

1.D；2.C；3.D；4.D；5.C；6.B；7.A；8.D；9.D；10.C

11.平行或在平面内；　 12. 平行或在平面内；　 13.4；　 14.若②③④则①

17.（2）45°