新课标人教A高一数学必修1测试题
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共10小题，每小题5分，共60分)
1.已知A={xy=x,x∈R},B={yy=x2,x∈R},则A∩B等于
A.{xx∈R} B.{yy≥0}
C.{(0,0),(1,1)} D.
2.方程x2-px+6=0的解集为M,方程x2+6x-q=0的解集为N,且M∩N={2},那么p+q等于
A.21 B.8 C.6 D.7
3. 下列四个函数中,在(0,+∞)上为增函数的是
A.f(x)=3-x B.f(x)=x2-3x
C.f(x)=-
D.f(x)=-x
4.函数f(x)=x2+2(a－1)x+2在区间(-∞,4］上递减,则a的取值范围是
A.［-3,+∞］ B.(-∞,-3)
C.(-∞,5］ D.［3,+∞)
5. 下列四个函数中,与y=x表示同一函数的是
A.y=(
)2 B.y=
C.y=
D.y=
6. 函数y=
+1(x≥1)的反函数是
A.y=x2-2x+2(x＜1) B.y=x2-2x+2(x≥1)
C.y=x2-2x(x＜1) D.y=x2-2x(x≥1)
7. 已知函数f(x)=
的定义域是一切实数,则m的取值范围是
A.0<m≤4 B.0≤m≤1 C.m≥4 D.0≤m≤4
8.某商场对顾客实行购物优惠活动，规定一次购物付款总额：
(1)如果不超过200元，则不给予优惠；
(2)如果超过200元但不超过500元，则按标价给予9折优惠；
(3)如果超过500元，其500元内的按第(2)条给予优惠，超过500元的部分给予7折 优惠.
某人两次去购物，分别付款168元和423元，假设他一次性购买上述两次同样的商品，则应付款是
A.413.7元 B.513.7元
C.546.6元 D.548.7元
9. 二次函数y=ax2+bx与指数函数y=(
)x的图象只可能是
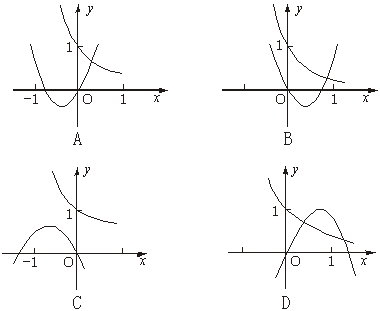
10. 已知函数f(n)=
其中n∈N，则f(8)等于
A.2 B.4 C.6 D.7
11．如图，设a,b,c,d>0，且不等于1，y=ax , y=bx , y=cx ,y=dx 在同一坐标系中的图象如图，则a,b,c,d的大小顺序（ ）
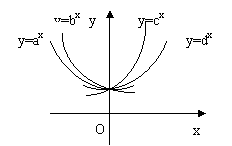A、a<b<c<d B、a<b<d<c
C、b<a<d<c D、b<a<c<d
12．.已知0<a<1,b<-1,函数f(x)=ax+b的图象不经过:（ ）
A.第一象限; B.第二象限; C.第三象限; D.第四象限
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共4小题，每小题5分，共20分)
13.已知f(x)=x2－1(x<0)，则f－1(3)=_______.
14． 函数
的定义域为______________
15.某工厂8年来某产品产量y与时间t年的函数关系如下图，则：
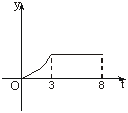
①前3年总产量增长速度增长速度越来越快；
②前3年中总产量增长速度越来越慢；
③第3年后，这种产品停止生产；
④第3年后，这种产品年产量保持不变.
以上说法中正确的是_______.
16. 函数y=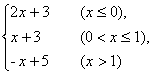
的最大值是_______.
三、解答题
17. 求函数y=
在区间［2,6］上的最大值和最小值.（10分）
18.(本小题满分10分) 试讨论函数f(x)=loga
(a＞0且a≠1)在(1,+∞)上的单调性,并予以证明.
答案
一. BACCB BDCAD BA 二。13. 2 ,14. 
, 15. ①④ 16. 4
三．17.解：设x1、x2是区间［2,6］上的任意两个实数,且x1<x2,则
f(x1)-f(x2)= 
-
=
=
.
由2<x1<x2<6,得x2-x1>0,(x1-1)(x2-1)>0,
于是f(x1)-f(x2)>0,即f(x1)>f(x2).
所以函数y=是区间［2,6］上的减函数.
因此,函数y=在区间的两个端点上分别取得最大值与最小值,即当x=2时,ymax=2;当x=6时,ymin=
.
18．解:设u=,任取x2＞x1＞1,则
u2－u1=
=
=
.
∵x1＞1,x2＞1,∴x1－1＞0,x2－1＞0.
又∵x1＜x2,∴x1－x2＜0.
∴＜0,即u2＜u1.
当a＞1时,y=logax是增函数,∴logau2＜logau1,
即f(x2)＜f(x1);
当0＜a＜1时,y=logax是减函数,∴logau2＞logau1,
即f(x2)＞f(x1).
综上可知,当a＞1时,f(x)=loga在(1,+∞)上为减函数;当0＜a＜1时,f(x)=loga在(1,+∞)上为增函数.