数学必修1第三章测试题
班别 姓名 学号 考分
一、选择题:本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 函数
的定义域是（ ）。
A. 
B. 
C. 
D. 
2. 函数
的图象过定点（ ）。
A.（1，2） B.（2，1） C.（-2，1） D.（-1，1）
3. 设
，则
的值为（ ）。
A. 128 B. 256 C. 512 D. 8
4. 
化简的结果是（ ）。
A. –a B.
C.
a D.
a
5. 函数
的反函数是（ ）。
A. 
B.
C. 
D.
6. 若
在（0，+∞）内为减函数，且
为增函数，则a的取值范围是（ ）。
A. 
B.
C.
D.
7. 设
，则a、b的大小关系是（ ）。
A.b＜a＜1 B. a＜b＜1 C. 1＜b＜a D. 1＜a＜b
8. 下列函数中，值域为（0，+∞）的函数是（ ）。
A. 
B.
C. 
D. 
9. 设偶函数
在[0，π]上递减，下列三个数a=
的关系为（ )。
A. a＞b＞c B. b＞a＞c C. b＞c＞a D. c＞a＞b
10. 已知0＜a＜1，b＞1，且ab＞1，则下列不等式中成立的是（ ）。
A. 
B.
C. 
D.
11. 定义运算
为：
如
，则函数
的值域为（ ）。
A. R B. （0，+∞） C. （0，1] D. [1，+∞）
12. 设a、b、c都是正数，且
，则以下正确的是（ ）。
A. 
B.
C.
D.
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上.
13. 
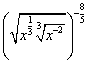化成分数指数幂为
。
14. 若不等式
成立，则x的取值范围是 ，a的取值范围是 。
15. 已知
，则m的取值范围是
。
16. 给出下列四种说法：
⑴ 函数
与函数
的定义域相同；
⑵ 函数
的值域相同；
⑶ 函数
均是奇函数；
⑷ 函数
上都是增函数。
其中正确说法的序号是 。
三、解答题：本大题共6小题，共74分. 解答应写出文字的说明，证明过程或演算步骤.
17. 已知
，且
，求a的值。
18. 已知函数
在区间[1，7]上的最大值比最小值大
，求a的值。
19. 已知指数函数
，当
时，有
，解关于x的不等式
。
20. 已知函数
。
⑴ 求的定义域；
⑵ 当a＞1时，判断函数的单调性，并证明你的结论。
21. 设
，若当
时，有意义，求a的取值范围。
22. 某商品在最近100天内的价格
与时间t的函数关系是：
销售量
与时间t的函数关系是： g(t)
= －
t + 
(0≤t≤100 , t∈N), 求这种商品的日销售额S(t)的最大值。
参考答案
一、DDBCB DBBBA CB
提示：1.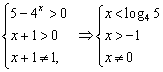 
故选D。
2. 代入验证。
3. 设
，则
，代入已知等式，得
。
4. 
5. 由，得
即
，两边取对数，得
，即。
6. 解不等式组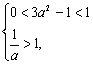
即可。
7. 由指数函数的性质，得0＜a＜1，0＜b＜1，又由幂函数
的性质知，当n＞0时，它在第一象限内递增，故a＜b＜1。
8. 在中
，∴ 
；在中，值域为（-1，+∞）；而的值域为[0，1）。
9. 由题意知，
，因为在[0，π]上递减，且
， ∴ 
， 即b＞a＞c。
10. 取
。
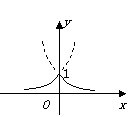
11. 由题意知，的结果为a、b中较小者，于是 的图象就是
的图象的较小的部分（如图），故值域为（0，1]。
12. 设
，则k＞0且k≠1，取对数得
，
∴ 
，
∴ 。
二、13. 
。提示：原式=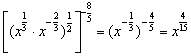
。
14. 
。提示：∵ 
且，
∴ 0＜a＜1。 由
，得
。
15. 
。提示：解不等式组
。
16. ⑴⑶。提示：⑴中两个函数的定义域都是R；⑵中两个函数的值域分别是R与（0，+∞）；⑶中两个函数均满足
，是奇函数；⑷中函数
在
不是增函数。
三、17. 解：因为
，两边取对数，得
，
所以
，解得
，
即
。
18. 解：若a＞1，则在区间[1，7]上的最大值为
，最小值为
，依题意，有
，解得a =
16；
若0＜a＜1，则在区间[1，7]上的最小值为，最大值为，依题意，有
，解得a =
。
综上，得a = 16或a =。
19. 解：∵ 在时，有， ∴ 
。
于是由，得
，
解得
， ∴ 不等式的解集为
。
20. 解：⑴ 由
，得
。
当a＞1时，解不等式，得
；
当0＜a＜1时，解不等式，得
。
∴ 当a＞1时，的定义域为
；当0＜a＜1时，的定义域为
。
⑵ 当a＞1时，在（-∞，0）上是减函数，证明如下：
设
是（-∞，0）内的任意两个数，且
，则
-
=
，
∵ a＞1，
， ∴ 
， ∴ 
。
从而
，即＞.
∴当a＞1时，在（-∞，0）上递减。
21. 解：根据题意，有
，，
即
，，
∵ 
在
上都是增函数，
∴ 
在上也是增函数，
∴ 它在
时取最大值为
，
即
，
∴ 
。
22. 解：因为
，所以
⑴ 当
，从而可知当
；
⑵ 
，当t = 40时， 
。
综上可得，
。
答：在最近的100天内，这种商品的日销售额的最大值为808.5。