不等式复习（3） 班级 姓名
1．已知点P（x，y）在不等式组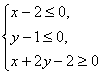
表示的平面区域上运动，则z＝x－y的取值
范围是 （ ）
A．[－2，－1] B．[－2，1] C．[－1，2] D．[1，2]
2. 变量x、y满足下列条件：
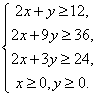则使z=3x+2y的值最小的（x，y）是
（ ）
A. ( 4.5 , 3 ) B. ( 3, 6 ) C. ( 9, 2 ) D. ( 6, 4 )
3．在坐标平面上，不等式组
所表示的平面区域的面积为 （ ）
A．
B．
C．
D．
4．设集合
, 
, 则A∩B= （ ）
A．
B．
C．
D．
5.不等式组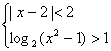
的解集为
( )
(A) (0, 
)； (B)
(, 2)； (C)
(, 4)； (D)
(2, 4)
6.在R上定义运算
若不等式
对任意实数
成立，则
A．
B．
C．
D．
（ ）
7．下列结论正确的是 （ ）
A．当
B．
C．
的最小值为2 D．当
无最大值
8．不等式
的解集为
（ ）
A. 
B.
C.
D.
9．设a＞0, b＞0，则以下不等式中不恒成立的是 （ ）
（A）
≥4
（B）
≥
（C）
≥
（D）
≥
10．已知
则
( )
A.
B.
C. 
D.
11．设集合
≤0},
那么点P(2,3) 
， 则
的取值范围是
( )
(A)m＞—1 ,n＜5 (B) m＜—1 ,n＜5
(C) m＞—1 ,n＞5 (D) m＜—1 ,n＞5
12．若
是正数，则
的最小值是
( )
A．3 B．
C．4 D．
13．函数y＝
的定义域是
。
14．非负实数满足
，则
的最大值为
。
15．设变量x、y满足约束条件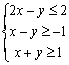
，则
的最大值为
16．已知在△ABC中，∠ACB=90°，BC=3，AC=4，P是AB上的点，则点P到AC、BC的距离乘积的最大值是
17．已知是正实数，且
，求证：
18．已知
为两个正常数，是正实数，且
，求
的最小值
19．已知：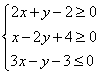
，求
的最值，并求出
取得最值时的的值。
20．.(2004江苏)制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.
某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？
21．某村计划建造一个室内面积为800m2的矩形蔬菜温室。在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？
答案及更正：
1．C
2．B
3．B
4．D
5．C
6．C
7．B
8．A
9．B
10．无解
11．A
12．C
13．
14．
更正为
，最大值为9
15．18
16．3
17．略
18．
19．的最大值为13，此时
；的最小值为
，此时
20．
解：
，设
当
时，取最大值7万元
21．当矩形温室的边长的左右长为20m，前后长为40m时，种植面积最大，最大种植面积为648m2.