第一章《空间几何体》
一、选择题
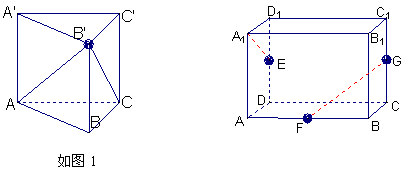
1． 已知高为3的直棱柱ABC—A′B′C′的底面是边长为1的正三角形（如图1所示），则三棱锥B′—ABC的体积为
A．
B．
C．
D．
 |
2．如图，长方体ABCD—A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是
A．
B．
C．
D．
3．如图，在三棱柱
中，点E、F、H、K分别为
、
、
、
的中点，G为ΔABC的重心
从K、H、G、
中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P为
A．K
B．H
C．G
D．
 |
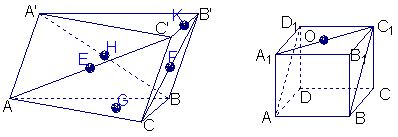4．如图，正方体ABCD－A1B1C1D1的棱长为1，O是底面A1B1C1D1的中心，则O到平面AB C1D1的距离为
A．
B．
C．
D．
5．木星的体积约是地球体积的
倍，则它的表面积约是地球表面积的
A．60倍 B．60
倍 C．120倍 D．120倍
6．在正三棱柱
中，若AB=2，
则点A到平面
的距离为
A．
B．
C．
D．
7．矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折成一个直二面角B－AC－D，则四面体ABCD的外接球的体积为
A．
B．
C．
D．
9．一个与球心距离为1的平面截球所得的圆面面积为
，则球的表面积为
A．
B．
C．
D．
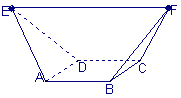10．如图，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且
均为正三角形，EF∥AB，EF=2，则该多面体的体积为
A．
B．
C．
D．
11．将半径都为１的４个钢球完全装入形状为正四面体的容器里，这个
正四面体的高的最小值为
A．
B．2+
C．4+ D．
12．
的顶点在平面
内，
、
在的同一侧，
、
与所成的角分别是
和
．若＝３，＝
，
＝５，则与所成的角为
A．
B． C．
D．
13．设三棱柱ABC-A1B1C1的体积为V，P、Q分别是侧棱AA1、CC1上的点，且PA=QC1，则四棱锥B-APQC的体积为
A．
B．
C．
D．
14．设地球半径为R，若甲地位于北纬
东经
，乙地位于南纬度
东经，则甲、乙两地球面距离为
A．
B． 
C．
D．
15．如图，在体积为1的三棱锥A—BCD侧棱AB、AC、AD上分别取点E、F、G， 使AE : EB=AF : FC=AG : GD=2 : 1，记O为三平面BCG、CDE、DBF的交点，则三棱锥O—BCD的体积等于
A．
B．
C． 
D．
 |
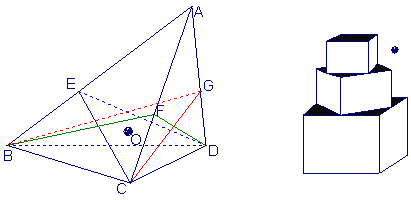16．有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各连接中点，已知最底层正方体的棱长为2，且该塔形的表面积（含最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是
A．4 B．5 C．6 D．7
二、填空题
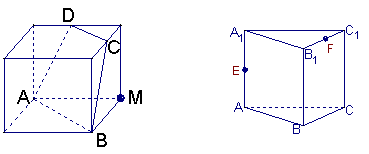
1．如图，正方体的棱长为1，C、D分别是两条棱的中点，A、B、M是顶点，那么点M到截面ABCD的距离是 .
 |
2．如图，在直三棱柱ABC—A1B1C1中，AB=BC=
，BB1=2，
，E、F分别为AA1、C1B1的中点，沿棱柱的表面从E到F两点的最短路径的长度为
.
3．如图，正方体
的棱长为
，将该正方体沿对角面
切成两块，再将这两块拼接成一个不是正方体的四棱柱，那么所得四棱柱的全面积为__________．
4．如图，在三棱锥P—ABC中，PA=PB=PC=BC，且
，则PA与底面ABC所成角为
.
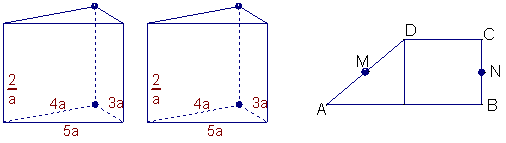
5．
有两个相同的直三棱柱，高为
，底面三角形的三边长分别为
、
、
。用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的一个是四棱柱，则的取值范围是_______
 |
6．设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E(如图)．现将△ADE沿DE折起，使二面角A－DE－B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小等于_________．
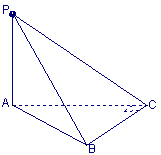7．如图，PA⊥平面ABC，∠ACB=90°且PA=AC=BC=a则异面直线PB与AC所成角的正切值等于________．
选择题、填空题答案
一、选择题
1．D 2．D 3．C 4．B 5．C 6．B 7．C 8．C
9．B 10．A 11．B 12．C 13．C 14．D 15．C 16．C
二、填空题
1．
2．
3． 
4．
5．
6． 
7．