(数学1必修)第一章(中) 函数及其表示
[基础训练A组]
一、选择题
1![]() 判断下列各组中的两个函数是同一函数的为( )
判断下列各组中的两个函数是同一函数的为( )
⑴![]() ,
,![]() ;
;
⑵![]() ,
,![]() ;
;
⑶![]() ,
,![]() ;
;
⑷![]() ,
,![]() ;
;
⑸![]() ,
,![]()
![]()
A![]() ⑴、⑵ B
⑴、⑵ B![]() ⑵、⑶ C
⑵、⑶ C![]() ⑷ D
⑷ D![]() ⑶、⑸
⑶、⑸
2![]() 函数
函数![]() 的图象与直线
的图象与直线![]() 的公共点数目是( )
的公共点数目是( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() 或
或![]() D
D![]()
![]() 或
或![]()
3![]() 已知集合
已知集合![]() ,且
,且![]()
使![]() 中元素
中元素![]() 和
和![]() 中的元素
中的元素![]() 对应,则
对应,则![]() 的值分别为( )
的值分别为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4![]() 已知
已知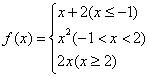 ,若
,若![]() ,则
,则![]() 的值是( )
的值是( )
A![]()
![]() B
B![]()
![]() 或
或![]() C
C![]()
![]() ,
,![]() 或
或![]() D
D![]()
![]()
5![]() 为了得到函数
为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象适当平移,
的图象适当平移,
这个平移是( )
A![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位 B
个单位 B![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位
个单位
C![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位 D
个单位 D![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位
个单位
6![]() 设
设![]() 则
则![]() 的值为( )
的值为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
二、填空题
1![]() 设函数
设函数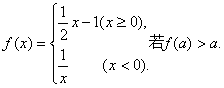 则实数
则实数![]() 的取值范围是
的取值范围是
![]()
2![]() 函数
函数![]() 的定义域
的定义域
![]()
3![]() 若二次函数
若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() ,且函数的最大值为
,且函数的最大值为![]() ,
,
则这个二次函数的表达式是
![]()
4![]() 函数
函数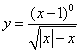 的定义域是_____________________
的定义域是_____________________![]()
5![]() 函数
函数![]() 的最小值是_________________
的最小值是_________________![]()
三、解答题
1![]() 求函数
求函数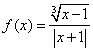 的定义域
的定义域![]()
2![]() 求函数
求函数![]() 的值域
的值域![]()
3![]()
![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实根,又
的两个实根,又![]() ,
,
求![]() 的解析式及此函数的定义域
的解析式及此函数的定义域![]()
4![]() 已知函数
已知函数![]() 在
在![]() 有最大值
有最大值![]() 和最小值
和最小值![]() ,求
,求![]() 、
、![]() 的值
的值![]()
(数学1必修)第一章(中) [基础训练A组]
参考答案
一、选择题
1![]() C (1)定义域不同;(2)定义域不同;(3)对应法则不同;
C (1)定义域不同;(2)定义域不同;(3)对应法则不同;
(4)定义域相同,且对应法则相同;(5)定义域不同;
2![]() C
有可能是没有交点的,如果有交点,那么对于
C
有可能是没有交点的,如果有交点,那么对于![]() 仅有一个函数值;
仅有一个函数值;
3![]() D 按照对应法则
D 按照对应法则![]() ,
,![]()
而![]() ,∴
,∴![]()
4![]() D 该分段函数的三段各自的值域为
D 该分段函数的三段各自的值域为![]() ,而
,而![]()
∴![]() ∴
∴ ![]() ;
;
1. D 平移前的“![]() ”,平移后的“
”,平移后的“![]() ”,
”,
用“![]() ”代替了“
”代替了“![]() ”,即
”,即![]() ,左移
,左移
6![]() B
B ![]()
![]()
二、填空题
1. ![]() 当
当![]() ,这是矛盾的;
,这是矛盾的;
当![]() ;
;
2![]()
![]()
![]()
3![]()
![]() 设
设![]() ,对称轴
,对称轴![]() ,
,
当![]() 时,
时,![]()
4![]()
![]()
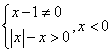
5![]()
![]()
![]()
![]()
三、解答题
1![]() 解:∵
解:∵![]() ,∴定义域为
,∴定义域为![]()
2![]() 解: ∵
解: ∵![]()
∴![]() ,∴值域为
,∴值域为![]()
3![]() 解:
解:![]() ,
,
![]()
![]()
∴![]()
![]()
4![]() 解:对称轴
解:对称轴![]() ,
,![]() 是
是![]() 的递增区间,
的递增区间,
![]()
![]()
∴![]()