高考数学一轮复习《函数》过关测试卷
时间 120分钟 总分 150分
一、选择题
1、若函数![]() 的图象过两点(-1,0)和(0,1),则
的图象过两点(-1,0)和(0,1),则
A a=2,b=2 B a=,b=2 C a=2,b=1 D a=,b=
2、设![]() ,用二分法求方程
,用二分法求方程![]() 内近似解的过程中
内近似解的过程中
得![]() 则方程的根落在区间
则方程的根落在区间
A (1,1.25) B (1.25,1.5) C (1.5,2) D 不能确定
3、若![]() ,当
,当![]() >1时,
>1时,![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、若函数![]() 在区间
在区间![]() 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则![]() =
=
A ![]() B
B ![]() C
C ![]() D
D ![]()
5、一元二次方程![]() 有一个正根和一个负根的充分不必要条件是:
有一个正根和一个负根的充分不必要条件是:
A ![]() B
B ![]() C
C ![]() D
D
![]()
6、![]() ,
,![]() ,
,![]() ,当
,当![]() 时,三个函数增长速度比较,下列选项
时,三个函数增长速度比较,下列选项
中正确的是
A ![]() >
>![]() >
>![]() B
B ![]() >
>![]() >
>![]()
C ![]() >
>![]() >
>![]() D
D ![]() >
>![]() >
>![]()
7、函数y=-ex的图象
A 与y=ex的图象关于y轴对称. B 与y=ex的图象关于坐标原点对称.
C 与y=e-x的图象关于y轴对称. D 与y=e-x的图象关于坐标原点对称.
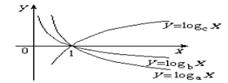
8、图中三条对数函数图象,若![]() ,则
,则![]() 的大小关系是
的大小关系是
A ![]() B
B ![]() C
C ![]() D
D ![]()
9、从任何一个正整数n出发,若n是偶数就除以2,若n是奇数就乘3再加1,如此继续下去…,现在你从正整数3出发,按以上的操作,你最终得到的数不可能是
班级__________ 姓名__________ 成绩__________
A 1 B 2 C 3 D 4
10、为了稳定市场,确保农民增收,某农产品的市场收购价格![]() 与其前三个月的市场收购价格有关,且使
与其前三个月的市场收购价格有关,且使![]() 与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
则7月份该产品的市场收购价格应为
A 69元 B 70元 C 71元 D 72元
11、正实数![]() 及函数
及函数![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为
A 4 B 2 C ![]() D
D ![]()
12、下列说法不正确的是
A 函数![]()
![]() 是奇函数
是奇函数
B 函数![]()
![]() 是偶函数
是偶函数
C 若![]() ,则
,则![]()
D 若![]()
![]() ,且
,且![]() ,则
,则![]()
二、填空题
13、已知![]() ,且
,且![]() ,则
,则![]() =_____________.
=_____________.
14、若M={-1,0,1} N={-2,-1,0,1,2}从M到N的映射满足:对每个x∈M恒使x+f(x) 是偶数, 则映射f有____个.
15、函数![]() 的零点有 个.
的零点有 个.
16、设函数![]() ,则不等式
,则不等式![]() 的解集是
.
的解集是
.
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
三、解答题
17、设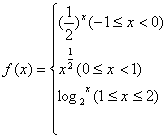 ,在同一坐标系中作出函数
,在同一坐标系中作出函数![]() 的图象.
的图象.
18、设![]() 是定义在[-1,1]上的奇函数,且其图象上任意两点连线的斜率均小于零.
是定义在[-1,1]上的奇函数,且其图象上任意两点连线的斜率均小于零.
(1)证明![]() 在[-1,1]上是减函数;
在[-1,1]上是减函数;
(2)如果![]() 的定义域的交集为空集,求实数
的定义域的交集为空集,求实数![]() 的取值范围;
的取值范围;
(3)证明:若 ![]() ,则
,则![]() 存在公共的定义域,并求出这个公共的定义域.
存在公共的定义域,并求出这个公共的定义域.
19、已知常数![]() , 变数x、y有关系
, 变数x、y有关系![]() .
.
(1)若![]()
![]() , 试以a、t表示y ;
, 试以a、t表示y ;
(2)若t在![]() 内变化时, y有最小值8,
求此时a和x的值各为多少?
内变化时, y有最小值8,
求此时a和x的值各为多少?
20、已知函数![]() ,且
,且![]()
(1)求![]() 的值;
的值;
(2)试判断是否存在正数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .若存在,求出这个
.若存在,求出这个![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
21、某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次,每日来回的次数是车头每次拖挂车厢个数的一次函数,每节车厢能载乘客110人. 问这列火车每天来回多少次,每次应拖挂多少车厢才能使运营人数最多?并求出每天最多运营人数.
22、已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(1)求函数f(x)的表达式;
(2)证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
参考答案
1-12 ABBAC BDBCC CD
13、0 14、12 15 1 16 ![]() 17 略
17 略
18、解: (1)由已知对任意的![]() 、
、![]()
![]() ,且
,且![]() ,都有
,都有![]() ,从而
,从而![]() 与
与
![]() 异号,所以
异号,所以![]() 在[-1,1]上是减函数.
在[-1,1]上是减函数.
(2)因为![]() 的定义域是
的定义域是![]() ,
,![]() 的定义域是
的定义域是![]() ,
,
因为以上两个集合的交集为空集,所以![]()
解得:![]()
(3)因为![]() 恒成立,有(2)问可知:当
恒成立,有(2)问可知:当![]() 时,
时,![]() 存在公共的定义域.
存在公共的定义域.
若![]() ,即
,即![]() 时,
时, ![]() ,此时的交
,此时的交
集是![]() ;
;
若![]() ,则
,则![]() ,此时的交集是
,此时的交集是![]()
19、解:(1) ![]()
![]() .
.
(2) ![]()
![]()
![]() 时,
时, ![]()
![]()
20、解:(1)∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]()
(2)![]() ,
, 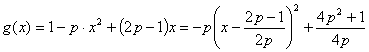
当![]() ,即
,即![]() 时,
时,![]()
当![]() 时,∵
时,∵![]() ,∴这样的
,∴这样的![]() 不存在。
不存在。
当![]() ,即
,即![]() 时,
时,![]() ,这样的
,这样的![]() 不存在。
不存在。
综上得,![]()
![]() .
.
21、解:设每日来回y次,每次挂x节车厢,由题意![]()
当x=4时y=16 当x=7时y=10得下列方程组:
![]() 16=4k+b
16=4k+b
10=7k+b
解得:k=![]() b=24
b=24 ![]()
![]()
由题意知,每日挂车厢最多时,营运人数最多,设每日营运S节车厢
则![]()
所以当![]() 时,
时,![]() 此时y=12
此时y=12
则每日最多运营人数为110×6×12=7920(人)
22、(Ⅰ)由已知,设f1(x)=ax2,由f1(1)=1,得a=1, ∴f1(x)= x2.设f2(x)=![]() (k>0),它的图象与直线y=x的交点分别为A(
(k>0),它的图象与直线y=x的交点分别为A(![]() ,
,![]() ),B(-
),B(-![]() ,-
,-![]() )
)
 由
由![]() =8,得k=8,. ∴f2(x)=
=8,得k=8,. ∴f2(x)=![]() .故f(x)=x2+
.故f(x)=x2+![]() .
.
(Ⅱ) (证法一)f(x)=f(a),得x2+![]() =a2+
=a2+![]() ,
,
即![]() =-x2+a2+
=-x2+a2+![]() .在同一坐标系内作出f2(x)=
.在同一坐标系内作出f2(x)=![]() 和
和
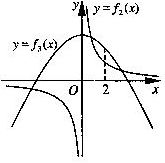
f3(x)= -x2+a2+![]() 的大致图象,其中f2(x)的图象是以坐
的大致图象,其中f2(x)的图象是以坐
标轴为渐近线,且位于第一、三象限的双曲线, f3(x)与的图象是以(0, a2+![]() )为顶点,开口向下的抛物线.因此, f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.又∵f2(2)=4, f3(2)= -4+a2+
)为顶点,开口向下的抛物线.因此, f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.又∵f2(2)=4, f3(2)= -4+a2+![]() ,当a>3时,. f3(2)-f2(2)= a2+
,当a>3时,. f3(2)-f2(2)= a2+![]() -8>0,当a>3时,在第一象限f3(x)的图象上存在一点(2,f(2))在f2(x)图象的上方.f2(x)与f3(x)的图象在第一象限有两个交点,即f(x)=f(a)有两个正数解.因此,方程f(x)=f(a)有三个实数解.
-8>0,当a>3时,在第一象限f3(x)的图象上存在一点(2,f(2))在f2(x)图象的上方.f2(x)与f3(x)的图象在第一象限有两个交点,即f(x)=f(a)有两个正数解.因此,方程f(x)=f(a)有三个实数解.
(证法二)由f(x)=f(a),得x2+![]() =a2+
=a2+![]() ,即(x-a)(x+a-
,即(x-a)(x+a-![]() )=0,得方程的一个解x1=a.方程x+a-
)=0,得方程的一个解x1=a.方程x+a-![]() =0化为ax2+a2x-8=0,由a>3,△=a4+32a>0,得x2=
=0化为ax2+a2x-8=0,由a>3,△=a4+32a>0,得x2=![]() , x3=
, x3=![]() ,x2<0, x3>0, ∵x1≠ x2,且x2≠
x3.若x1= x3,即a=
,x2<0, x3>0, ∵x1≠ x2,且x2≠
x3.若x1= x3,即a=![]() ,则3a2=
,则3a2=![]() , a4=4a,得a=0或a=
, a4=4a,得a=0或a=![]() ,这与a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三个实数解.
,这与a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三个实数解.