高一数学上册第二章测试题
A卷
1.下列命题中为真命题的是 ( )
A.平行直线的倾斜角相等 B.平行直线的斜率相等
C.互相垂直的两直线的倾斜角互补 D.互相垂直的两直线的斜率互为相反
2. 在同一直角坐标系中,表示直线![]() 与
与![]() 正确的是
( )
正确的是
( )
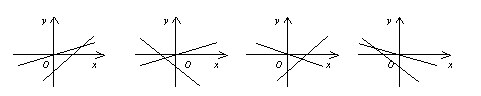
A. B. C. D.
图1
3.已知点![]() 、
、![]() ,则线段
,则线段![]() 的垂直平分线
的垂直平分线![]() 的方程是
( )
的方程是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如果直线![]() 与直线
与直线![]() 平行,那么系数
平行,那么系数![]() 为
( )
为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.空间直角坐标系中,点![]() 和点
和点![]() 的距离是
( )
的距离是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.圆:![]() 上的点到直线
上的点到直线![]() 的距离最大值是 ( )
的距离最大值是 ( )
A.2
B.![]() C.
C.![]() D.
D.![]()
7.直线![]() 关于
关于![]() 轴对称的直线方程为
.
轴对称的直线方程为
.
8.已知点![]() 和直线
和直线![]() :
:![]() ,则过P与直线
,则过P与直线![]() 平行的直线方程是
,过点P与
平行的直线方程是
,过点P与![]() 垂直的直线方程是
.
垂直的直线方程是
.
9.直线l经过直线![]() 和
和![]() 的交点,且在两坐标轴上的截距相等,则直线l的方程是_____ _.
的交点,且在两坐标轴上的截距相等,则直线l的方程是_____ _.
10.方程![]() 表示一个圆,则
表示一个圆,则![]() 的取值范围是
.
的取值范围是
.
11.求经过点![]() 且到原点的距离等于1的直线方程.
且到原点的距离等于1的直线方程.
12.已知一曲线是与两个定点![]() 、
、![]() 距离的比为
距离的比为![]() 的点的轨迹,则求此曲线的方程.
的点的轨迹,则求此曲线的方程.
B卷
1.过直线![]() 与
与![]() 的交点,且与第一条直线垂直的直线
的交点,且与第一条直线垂直的直线![]() 的方程是( )
的方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() ,则下列说法中正确的是
( )
,则下列说法中正确的是
( )
A.![]() 三点可以构成直角三角形 B.
三点可以构成直角三角形 B. ![]() 三点可以构成锐角三角形
三点可以构成锐角三角形
C. ![]() 三点可以构成钝角三角形 D.
三点可以构成钝角三角形 D. ![]() 三点不能构成任何三角形
三点不能构成任何三角形
3.已知![]() :
:![]() 和
和![]() :
:![]() 交于
交于![]() 两点,则
两点,则![]() 的垂直平分线的方程是
( )
的垂直平分线的方程是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.两点![]() 、B
、B![]() 关于直线
关于直线![]() 对称,则
( )
对称,则
( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
5.与圆![]() 相切,并在
相切,并在![]() 轴、
轴、![]() 轴上的截距相等的直线共有 ( )
轴上的截距相等的直线共有 ( )
A、6条 B、5条 C、4条 D、3条
6.直线![]() 被圆
被圆![]() 所截得的弦长等于
所截得的弦长等于![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A、-1或-3 B、![]() C、1或3 D、
C、1或3 D、![]()
7.已知![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() ,则点
,则点![]() 的坐标为
的坐标为
8.圆心在直线![]() 上的圆C与
上的圆C与![]() 轴交于两点
轴交于两点![]() ,
,![]() ,则圆C的方程为 .
,则圆C的方程为 .
9.已知点![]() 在直线
在直线![]() 上,则
上,则![]() 的最小值为
的最小值为
10.经过![]() 和直线
和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上的圆的方程为
.
上的圆的方程为
.
11.求垂直于直线![]() ,且与两坐标轴构成周长为10的三角形的直线方程
,且与两坐标轴构成周长为10的三角形的直线方程
12.自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
C卷
1.如图2,圆![]() 内有一点
内有一点![]() ,
,![]() 为过点
为过点![]() 且倾斜角为
且倾斜角为![]() 的弦,
的弦,
(1)当![]() =1350时,求
=1350时,求![]() ;(2)当弦
;(2)当弦![]() 被点
被点![]() 平分时,求出直线
平分时,求出直线![]() 的方程;
的方程;
(3)设过![]() 点的弦的中点为
点的弦的中点为![]() ,求点
,求点![]() 的坐标所满足的关系式.
的坐标所满足的关系式.
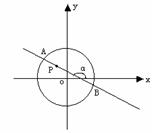
图2
2.设有半径为3![]() 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
参考答案
A卷
1. 解析:当直线的倾斜角为![]() ,斜率不存在时, B、C、D均不成立,选A.
,斜率不存在时, B、C、D均不成立,选A.
2. 解析:分别讨论![]() 两种情况,选C.
两种情况,选C.
3. 解析:∵![]() ,∴
,∴![]() ,又
,又![]() 中点
中点![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ,选B.
,选B.
4. 解析:由![]() 可求得
可求得![]() ,选B.
,选B.
5. 解析:代入两点间的距离公式可得:![]() ,选D.
,选D.
6. 解析:圆![]() 可化为标准形式:
可化为标准形式:![]() ,其圆心(1,1)到直线
,其圆心(1,1)到直线![]() 的距离
的距离![]() ,则所求距离最大为
,则所求距离最大为![]() ,选B.
,选B.
7. 解析:![]() .
.
8. 解析:![]() 或
或![]() .
.
9.解析:![]() 或
或![]() .
.
10. 解析:![]() .
.
11. 解:(1)当过点![]() 的直线与
的直线与![]() 轴垂直时,则点
轴垂直时,则点![]() 到原点的距离为1,所以
到原点的距离为1,所以![]() 为所求直线方程.
为所求直线方程.
(2)当过点![]() 且与
且与![]() 轴不垂直时,可设所求直线方程为
轴不垂直时,可设所求直线方程为![]() ,
,
即:![]() ,由题意有
,由题意有![]() ,解得
,解得![]() ,
,
故所求的直线方程为![]() ,即
,即![]() .
.
综上,所求直线方程为![]() 或
或![]() .
.
12. 解:在给定的坐标系里,设点![]() 是曲线上的任意一点,则
是曲线上的任意一点,则![]()
由两点间的距离公式,点![]() 所适合的条件可以表示为
所适合的条件可以表示为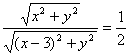 ,
,
两边平方,得![]() ,化简整理有:
,化简整理有:![]() ,
,
化为标准形式:![]() ,所以,所求曲线是以C(-1,0)为圆心,2为半径的圆.
,所以,所求曲线是以C(-1,0)为圆心,2为半径的圆.
B卷
1. 解析:由![]() 可得两直线交点
可得两直线交点![]() ,又
,又![]() ,∴所求直线
,∴所求直线![]() 方程为:
方程为:![]() ,即
,即![]() ,选B.
,选B.
2. 解析:∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,选A.
,选A.
3. 解析:∵![]() ,
,![]() ,由题意知
,由题意知![]() 的垂直平分线即为经过
的垂直平分线即为经过![]() 的直线,可求得其方程为:
的直线,可求得其方程为:![]() ,选C.
,选C.
4. 解析:由题意可知:![]() 连线同直线
连线同直线![]() 垂直,
垂直,![]() 中点在直线
中点在直线![]() 上,则有
上,则有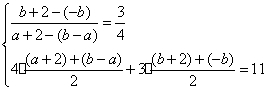 ,可解得
,可解得![]() ,选C.
,选C.
5. 解析:画图易知选D.
6. 解析:设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则由题意有
,则由题意有![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() 或
或![]() ,选C.
,选C.
7. 解析:设![]() ,则由
,则由![]() ,可解得
,可解得![]() ,∴
,∴![]()
8. 解析:由题意知圆C的圆心为![]() 的中垂线
的中垂线![]() 与直线
与直线![]() 的交点,可求得
的交点,可求得![]() ,再进一步可求得半径
,再进一步可求得半径![]() ,∴所求圆的方程为:
,∴所求圆的方程为:![]() .
.
9. 解析:![]() 的最小值即为以
的最小值即为以![]() 为圆心,同直线
为圆心,同直线![]() 相切的圆的半径,又即
相切的圆的半径,又即![]() 到直线
到直线![]() 的距离
的距离![]() ,则
,则![]() 的最小值为3.
的最小值为3.
10. 解析:设所求圆的方程为:![]() ,又此圆经过点
,又此圆经过点![]() 且和直线
且和直线![]() 相切,则有
相切,则有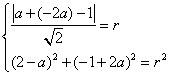 ,可解得
,可解得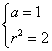 ,
,
∴所求圆的方程为![]() .
.
11. 解:由所求直线能与坐标轴围成三角形,则所求直线在坐标轴上的截距不为0,故可设该直线在![]() 轴、
轴、![]() 轴上的截距分别为
轴上的截距分别为![]() ,又该直线垂直于直线
,又该直线垂直于直线![]() ,且与两坐标轴构成周长为10的三角形,故有
,且与两坐标轴构成周长为10的三角形,故有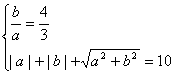 ,
,
解得: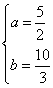 或
或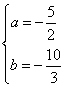 ,所以所求直线方程为
,所以所求直线方程为![]() 或
或![]() .
.
12.
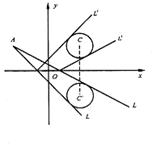
如图3
解法一:如图3,已知圆的标准方程是:(x-2)2+(y-2)2=1,它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1.设光线L所在的直线的方程是y-3=k(x+3)(其中斜率k待定),由题设知对称圆的圆心C′(2,-2)到这条直线的距离等于1,即d=![]() =1.整理得:12k2+25k+12=0,解得k= -
=1.整理得:12k2+25k+12=0,解得k= -![]() 或k= -
或k= -![]() .故所求直线方程是y-3= -
.故所求直线方程是y-3= -![]() (x+3),或y-3=
-
(x+3),或y-3=
-![]() (x+3),即3x+4y+3=0或4x+3y+3=0.
(x+3),即3x+4y+3=0或4x+3y+3=0.
解法二:已知圆的标准方程是:(x-2)2+(y-2)2=1,设光线L所在的直线的方程是:y-3=k(x+3)(其中斜率k待定),由题意知k≠0,则L的反射点的坐标是(-![]() ,0),因为光线的入射角等于反射角,所以反射光线
,0),因为光线的入射角等于反射角,所以反射光线![]() 所在直线的方程为y= -k(x+
所在直线的方程为y= -k(x+![]() ),即y+kx+3(1+k)=0.这条直线与已知圆相切,故圆心到直线的距离为1,即d=
),即y+kx+3(1+k)=0.这条直线与已知圆相切,故圆心到直线的距离为1,即d=![]() =1.以下同解法一.
=1.以下同解法一.
C卷
1. 解:(1)过点![]() 做
做![]() 于
于![]() ,连结
,连结![]() ,当
,当![]() =1350时,直线
=1350时,直线![]() 的斜率为-1,故直线
的斜率为-1,故直线![]() 的方程x+y-1=0,∴OG=d
的方程x+y-1=0,∴OG=d![]() ,又∵r=
,又∵r=![]() ,
,
∴![]() ,∴
,∴ ![]() ,
,
(2)当弦![]() 被
被![]() 平分时,
平分时,![]() ,此时KOP=
,此时KOP=![]() ,
,
∴![]() 的点斜式方程为
的点斜式方程为![]() .
.
(3)设![]() 的中点为
的中点为![]() ,
,![]() 的斜率为K,
的斜率为K,![]() ,则
,则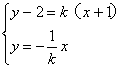 ,
,
消去K,得:![]() ,当
,当![]() 的斜率K不存在时也成立,故过点
的斜率K不存在时也成立,故过点![]() 的弦的中点的轨迹方程为:
的弦的中点的轨迹方程为:![]() .
.
2. 解:
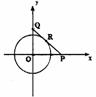
图4
如图4,建立平面直角坐标系,由题意可设A、B两人速度分别为3v千米/小时 ,v千米/小时,再设出发x0小时,在点P改变方向,又经过y0小时,在点Q处与B相遇.则P、Q两点坐标为(3vx0, 0),(0,vx0+vy0).由OP2+OQ2=PQ2知,(3vx0)2+(vx0+vy0)2=(3vy0)2,
即![]() .
.![]() ……①
……①
将①代入![]()
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线![]() 相切,则有
相切,则有![]()
答:A、B相遇点在离村中心正北![]() 千米处.
千米处.