高一数学上学期模块测试题(必修1部分)
说明:本试题分第I卷和第II卷两部分,满分120分,时间90分钟
一、 选择题:本大题共12小题,每小题5分共计60分。
1.集合P={xx2-1=0},T={-1,0,1},则P与T的关系为( )
![]()
![]()
![]() A. P T B. P T C. P = T D. P T
A. P T B. P T C. P = T D. P T
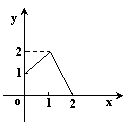
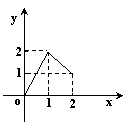 2.设A={x
2.设A={x![]() },B={y1
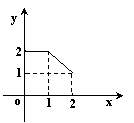
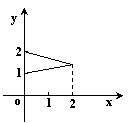
},B={y1![]() },下列图形表示集合A到集合B的函数图形的是( )
},下列图形表示集合A到集合B的函数图形的是( )
A B C D
3.设![]() ,则a,b,c大小关系( )
,则a,b,c大小关系( )
A. a>c>b B. c>a>b C. a>b>c D.b>a>c
4.下列图像表示的函数能用二分法求零点的是( )
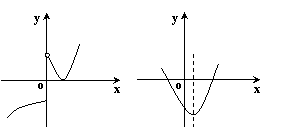 | |||||
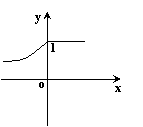 | 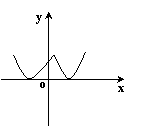 | ||||
A B C D
5.已知![]() ,则
,则![]() ( )
( )
A .![]() B.
8 C.
18
D .
B.
8 C.
18
D .![]()
6.已知![]() 0是定义在(
0是定义在(![]() 上的单调增函数,若
上的单调增函数,若![]() ,则x的范围是( )
,则x的范围是( )
A x>1 B. x<1 C.0<x<2 D. 1<x<2
7.若函数![]() 对任意实数都有
对任意实数都有![]() ,则( )
,则( )
A ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
8.设函数![]() 上单调递增,则
上单调递增,则![]() 的大小关系为( )
的大小关系为( )
A
![]() B
B ![]() C.
C. ![]() D.不确定
D.不确定
9.已知集合A={5,6,7,8},设f,g都是由A到A的映射,其对应法则分别如下表1和表2所示:
| 原象 | 5 | 6 | 7 | 8 | |||||
| 表象 | 7 | 8 | 6 | 5 | |||||
| 原象 | 5 | 6 | 7 | 8 | |||||
| 象 | 7 | 8 | 6 | 5 | |||||
表1 表2
则与f〔g(5)〕的值相同的为( )
A.g〔f(5)〕 B.g〔f(6)〕 C .g〔f(7)〕 D. g[f(8)]
10.函数 f(x)=x2-4x+5在区间 [0,m]上的最大值为5,最小值为1,则m的取值范围是( )
A . ![]() B
.[2,4]
C .(
B
.[2,4]
C .(![]() D。[0,2]
D。[0,2]
11.设![]() 则关于x的函数f(x)=
则关于x的函数f(x)=![]() 为( )
为( )
A .奇函数且非偶函数 B.偶函数且非奇函数 C.既奇且偶函数 D.非奇非偶函数
12.某公司在甲乙两地同时销售一种品牌车,利润(单位:万元)分别为L1=-x2+21x和L2=2x其中
销售量(单位:辆)若该公司在两地共销售15辆,则能获得的最大利润为( )万元
A .90 B.60 C.120 D.120.25
二、填空题:本大题共4个小题,每小题4分共16分
13.如果指数函数![]() 是R上的间函数,则a的取值范围是 ___________.
是R上的间函数,则a的取值范围是 ___________.
14.已知![]() ,则
,则![]() ___________.
___________.
![]() 15.若集合A {2,3,7},且A中之多有1个奇数,则这样的集合共有__________.
15.若集合A {2,3,7},且A中之多有1个奇数,则这样的集合共有__________.
16.如图是某企业几年来关于生产销售的一张统计表,关于改企业近几年的销售情况有一下几种说法:
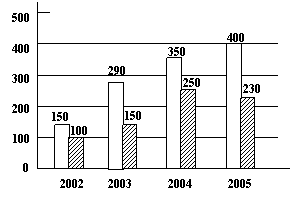 (1)这几年该企业的利润逐年提高
(1)这几年该企业的利润逐年提高
(注:利润=销售额-总成本)
(2)2002年至2003年是该企业的销售额增长
最快的一年;
(3)2003年至2004年是该企业销售额增长最慢
的一年;
(4)2004年至2005年该企业销售额增长最慢,
但由于总成本由所下降,因而2005年该企业
的利润比上一年仍由所增长。
其中说法正确的是_________
( 注:把你认为正确说法的序号都填上)
第II卷
三、解答题:本大题共6道小题,共54分,解答应写出文字说明,说明过程或验算步骤:
17、本小题满分8分
已知全集U=![]() ,集合A={
,集合A={![]() ,集合B=
,集合B=![]()
求(1)![]() (2) (
(2) (![]() )
)![]() (3)
(3) ![]()
18.(本小题8分)
已知函数![]() 若f(x)满足f(-x)=-f(x)
若f(x)满足f(-x)=-f(x)
(1) 求实数a的值;
(2) 判断病症明函数f(x)的单调性。
19.(本小题9分)
已知![]() 。
。
(1) 求f(x)的解析是,并写出定义域;
(2) 判断f(x)的奇偶性并证明;
(3)
当a>1时,求使f(x)![]() 成立的x的集合。
成立的x的集合。
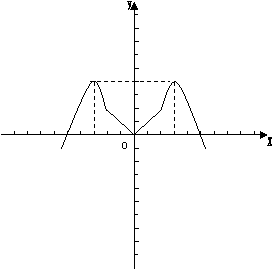
20.设f(x)为定义在R上的偶函数,当![]() 时,y=x;当x>2时,y=f(x)的图像时顶点在P(3,4),
时,y=x;当x>2时,y=f(x)的图像时顶点在P(3,4),
 且过点A(2,2)的抛物线的一部分
且过点A(2,2)的抛物线的一部分
(1)
求函数f(x)在![]() 上的解析式;
上的解析式;
(2) 在下面的直角坐标系中直接画出函数f(x)的图像;
(3) 写出函数f(x)值域。
21.(本小题10分)
对于函数f(x),若存在![]() ,使f(xo)=xo成立,则xo为f(x)的不动点;
,使f(xo)=xo成立,则xo为f(x)的不动点;
已知f(x)=ax2+(b+1)x+(b-1)
(![]()
(1) 当a=1,b=-2时,求f(x)的不动点;
(2)
若对于![]() ,函数f(x)恒有两个互异的不动点,求实数a的取值范围。
,函数f(x)恒有两个互异的不动点,求实数a的取值范围。
22.(本小题满分10分)
经市场调查,某种商品在120天内的日销售量和售价均为时间t(天)的函数,日销售量与时间的关系用图(1)的一条折线表示,售价与时间的关系用图(2)的一条折线表示。
(1) 写出图(1)表示的日销售量(千克)与时间t的函数关系史Q=g(t);写出图(2)表示的售价(元 /千克)与时间t的函数关系式P=f(t);
(2)
|
|

 求日销售额y(元)与时间的函数关系式,并求出日销售额最高的时哪一天?最高的销售额时多少?(注:日销售额=日销售量×售价)
求日销售额y(元)与时间的函数关系式,并求出日销售额最高的时哪一天?最高的销售额时多少?(注:日销售额=日销售量×售价)
潍坊市2006年高一数学模块测试题参考答案
一. 选择题:(每小题4分,共48分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | C | C | D | D | A | B | A | B | A | C |
二、填空题:(每小题4分,共16分)
13. 1<a<2 ; 14. -1 ; 15. 6; 16. ②④
三.解答题:
17.解:(1)![]() ={3,4}
(2) (
={3,4}
(2) (![]() )
)![]() ={1,3,4,5,6} (3)
={1,3,4,5,6} (3) ![]() ={1,6}
={1,6}
18.解:(1)a=1 (2)![]() 在R上为单调增函数。
在R上为单调增函数。
19.解:(1)解析式为![]() 定义域为
定义域为![]()
(2)![]() 为奇函数
为奇函数
证明:![]()
![]() =
=![]() =-
=-![]() =-
=-![]()
![]() 为奇函数。
为奇函数。
(3)
 使
使![]() 成立的x的集合为{x0≤x<5}
成立的x的集合为{x0≤x<5}
20.解:(1)当![]() 时解析式为
时解析式为![]()
(2) 图像如右图所示。
(3)值域为:![]()
21.解:(1)f(x)的不动点为3或-1
(2)a的范围0<a<1
22.解:(1)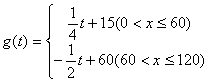
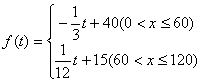
(2)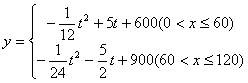
当![]() 时
时
![]()
当x=30时ymax=675;
当![]() 时
时
![]() 因为当
因为当![]() 时函数单调递减
时函数单调递减
所以ymax <615
综上所述:在第30天的时候销售额最大,最高额为675元。