高一数学竞赛试题（新课程）
班别 姓名 分数
（时间：100分钟, 满分150分）
一、选择题(共6小题,每小题6分,共48分)
1、集合｛0,1，2，2006｝的非空真子集的个数是 （ ）
（A）16 （B）15 （C）14 （D）13
2、设U=Z，M=
，N=
，P=
，则下列结论不正确的是 （ ）
(A)
(B)
(C) 
(D) 
3、根据图中骰子的三种不同状态显示的数字，推出？处的数字是（ ）
(A)1 (B)2 (C)3 (D)6
5
1
?
4 1 2 3 4 5
4、函数
的图象是 （ ）
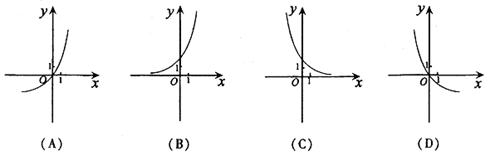
5、函数
上的最大值和最小值之差为
,
则的
值为 (
)
(A )2或
(B)2或4 (C)或4 (D)2
6、有A、B、C、D、E共5位同学一起比赛象棋，每两人之间只比赛1盘，比赛过程中统计比赛的盘数知：A赛了4盘，B赛了3盘，C赛了2盘，D赛了1盘，则同学E赛了（）盘
（A）1 （B）2 （C）3 （D）4
7若
的解是
,则a和c的值是（ ）
(A)a=6,c=1 (B)a=6,c=-1 (C)a=-－6,c=1 (D)a=－6,c=-－1
8、若x=
, 
则xy的值为（ ）
(A) 12 (B)13 (C)14 (D)15
二、填空题（共6小题,每小题7分,共42分）
1、已知函数
，奇函数
在
处有定义，且
时，
，则方程
的解是
。
2、、吴川市的出租车按如下方法收费：起步价5元，可行3 km (不含3km)；超过3 km按
1.2元/km计价（不足1 km按1 km计算）。有一天，老李从吴川坐出租车到谭巴
（路程20 km多一点）。他得付车费 元（精确到1元）。
3、用火柴棒按下图的方法搭三角形:
按图示的规律搭下去,则第2006个图形所用火柴棒的支数为 支。
4、巳知f(x+y)=f(x) ﹒f(y),f(1)=2,则
____________.
5、设集合
，
，且
，则实数的取值范围是
。
6、设集合A={-1,1},B={x
-2ax+b=0},若B≠￠ 且B
A，则a 、b的值为__________
三、解答题（共3小题,每小题20分，共60分）
13、甲、乙两人到物价商店购买商品，商品里每件商品的单价只有8元和9元两种．已知两人购买商品的件数相同，且两人购买商品一共花费了172元，求两人共购买了两种商品各几件？
14已知二次函数y=+2(a-2)x+4,如果对x [-3,1],y>0成立，求a的取值范围。
15、设k为正整数，使得
也是一个正整数，求k的值。
〔解〕：
参考答案
一、1C 2B 3D 4C 5A 6B 7D 8C
二、1、
， 2、27， 3、4013 4 、3994， 5、
6、
或
或
三、13解：设每人购买了
件商品，两人共购买了单价为8元的
件，单价为9元的有
件．则
解之，得
因为
，所以
．
所以整数
．
故
14、解：（1）当-3
2-a1 即1a5 时 ,(2-a)
+2(a-2)(2-a)+4>0, 得
<0.所以0<a<4，结合1a5得1a<4.
（2）当2-a<-3即 a>5时,x=-3时,y的值最小。
所以(-3)+2(a-2)(-3)+4>0,
得a<
,结合a>5知a无解
（3）当2-a>1即a<1时,当x=1时，y的值最小，所以
+2(a-2)×1+4>0，得a>-，结合a<1得-<a<1。取(1)(2)(3)中a的取值集合的并集，得a的取值范围是{a-<a<4}。
15、解:令
,得
,
令
得
与
均为偶数.
(1) 若
均为偶数,令
,则
得
,
,
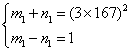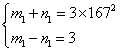或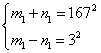
或
或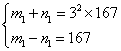
由
,得m=251002或m=83670或m=27898或m=1670.
这时,k=252004或84672或28900或2672。
(2) 若均为奇数,令
则
为奇数,得
与
均为奇数,矛盾!
这时无解.
综上所述,k的值为252004或84672或28900或2672。