高一数学下学期3月份月考试题
数 学
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．某单位有老年人28 人，中年人54人，青年人81人，为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本，则老年人、中年人、青年人分别各抽取的人数是 （ ）
A．6， 12 ，18 B．7，11，19 C．6，13，17 D．7，12，17
2．某射手射中10环、9环、8环的概率分别为0.24，0.28，0.19，那么，在一次射击训练中，该射手射击一次不够8环的概率是 （ ）
A．0.19 B．0.48 C． 0.29 D．0.71
3．给出以下四个问题：①输入一个正数x，求它的常用对数值； ②求面积为6的正方形的周长；③求三个数a,b,c中的最大数；④求函数
的函数值．其中不需要用条件语句来描述其算法的有
（ ）
A．1个 B．2个 C．3个 D． 4个
4．10名工人某天生产同一零件，生产的件数分别是15，17，14，10，15，17，17，16，14，12．设其平均数为a，中位数为b，众数为c，则有 （ ）
A．a>b>c B．b>c>a C．c>a>b D．c>b>a
5．下列抽样：①从标有1～15号的15个小球中，任选3个作为样本，按从小号到大号排序，随机选取起始号
，再取
，
号入样（超过15号时从1号再循环数起）；②工厂生产的产品，用传送带将产品送入包装车间，检验人员从传送带上每隔6分钟抽取1件产品进行检验； ③搞一项市场调查，规定在市场门口随机地抽取顾客进行调查，直到调查到事先预定的人数为止；④为了调查观众对影片的评价，通知每排（假定每排的观众数相等）座位号为18号的观众留下座谈．以上抽样中是系统抽样的是 （ ）
A．①②③④ B．①②④ C．②④ D．④
6．一批产品中，有10件正品和5件次品，对产品逐个进行检测，如果已检测到前3次均为正品，则第4次检测的产品仍为正品的概率是 （ ）
A．7/12 B． 4/15 C．6/11 D．1/3
7．某小组有6人，血型情况分别是：A型血3人，B型血2人，AB型血1人．如果从这个小组随机地抽取2人，那么，他们具有不同血型的概率是 （ ）
A．
B．
C．
D．
8．一枚骰子连续掷了两次，则点数之和为2或3的概率是 （ ）
A．
B．
C．
D．
9．如图所示的算法语句运行的结果
是 （ ）
A．1,2,3 B．2,3,1
C．2,3,2 D．3,2,1
10．如右图所示的算法语句输出的结
果是 （ ）
A．－1 B．0 C．1 D．2
11．算法:
S1 m a
S2 若b<m，则m b
S3 若c<m，则m c
S4 若d<m，则m d
S5 输出m
则输出的m表示
A．a，b，c，d中最大值
B．a，b，c，d中最小值
C．将a，b，c，d由小到大排序
D．将a，b，c，d由大到小排序
12．右面的伪代码输出的结果是
A．9 B．5
C．3 D．1
二、填空题（本大题共5小题，每小题5分，
共25分）
13．一个容量为20的样本数据，分组后，组
距与频数如下：
，2；
，3 ；
，4 ；
，5 ；
，
4；
，2．则该样本在区间
上
的频率为______.
14．有一个简单的随机样本：10，12， 9， 14，
15 则样本平均数
=______ ,样本方差
=______ .
15．有一个水平放置的半径为4的圆，现将一枚直径为2的硬币投向其中（硬币完全落在圆
外的不计），则硬币完全落在圆内的概率为 .
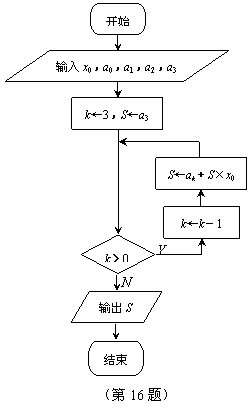
16．右图所示的算法流程图输出的结果S的意义是 .
17．算法语句：
 |
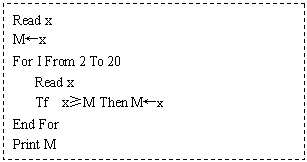的意义是 ．
三、解答题（本大题共6小题，共65分，18～21题每题10分，22题13分，23题12分；解题应写出文字说明，证明过程或演算步骤）
18．用计算机随机产生的有序二元数组
，满足
，
，对每个有序二元数组，用计算机计算
的值，记
为事件“
”．试求事件发生的概率．
19．某地随机抽查了140名成年男性的红细胞数（1012个/L），数据的分组及频数如表所示：
| 分 组 | 频 数 | 频 率 |
| [3.8，4.0 | 2 | |
| [4.0，4.2 | 6 | |
| [4.2，4.4 | 11 | |
| [4.4，4.6 | 25 | |
| [4.6，4.8 | 32 | |
| [4.8，5.0 | 27 | |
| [5.0，5.2 | 17 | |
| [5.2，5.4 | 13 | |
| [5.4，5.6 | 4 | |
| [5.6，5.8 | 2 | |
| [5.8，6.0 | 1 | |
| 合 计 | 140 |
（1）完成左边的频率分布表；
（2）根据频率分布表画出频率分布
直方图；
（3）试估计成年男性红细胞数在正
常值（4.0～5.5）的概率．
20．试设计解一元二次不等式ax2＋bx＋c≤0（a＞0）的算法流程图，并写出伪代码．
21．现欲从有6名同学的某小组中随机地抽取2人作为代表参加某项活动．
该小组的李平和王芳对该问题有下列一段对话：
李平：我希望第二次被抽到，因为第一次被抽到的概率是，而第二次被抽到的概率是
；
王芳：你说的不对．分两次抽时，第一次被抽到的概率是，第二次被抽到的概率还是
．我希望一次同时抽取2人，而不是分两次抽取，因为，一次同时抽取两人时每人被
抽到的概率是
．
试用你所学的有关知识，判断李平与王芳的观点是否正确，并说明理由．
22．用伪代码及算法流程图写出下列问题的一个算法：求满足
>2006的最小正整数n．
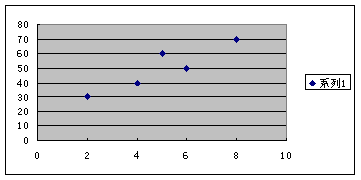
23． 某广告公司的广告费支出
与销售额
（单位：百万元）之间有下列对应数据：
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）试用最小二乘法推导出线性回归方程（注意：不得直接利用线性回归方程公式）．
数学参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | B | D | B | A | D | A | C | B | B | A |
13．0．3； 14．12，5．2； 15．
；
16．求多项式
当x＝x0时的值（或用秦九韶算法计算三次多项式的值）；
17．求给定的20个数的最大值；
18．解：在直角坐标系中，坐标满足，的点所在的区域
是由直线
，
，
，
围成的正方形的内部，
………………2分
此正方形的边长为2，所以区域的面积为4；
………………4分
坐标满足的点所在的区域
为以原点为圆心，
1为半径的圆的内部， ………………6分
所以区域的面积为
.
………………8分
所以
.
………………10分
19．解：（1）频率分布表如下表所示： ………………3分
| 分 组 | 频 数 | 频 率 | 频率/组距 |
| [3.8，4.0 | 2 | 0.014 | 0.07 |
| [4.0，4.2 | 6 | 0.043 | 0.21 |
| [4.2，4.4 | 11 | 0.079 | 0.39 |
| [4.4，4.6 | 25 | 0.179 | 0.89 |
| [4.6，4.8 | 32 | 0.229 | 1.14 |
| [4.8，5.0 | 27 | 0.193 | 0.96 |
| [5.0，5.2 | 17 | 0.121 | 0.61 |
| [5.2，5.4 | 13 | 0.093 | 0.46 |
| [5.4，5.6 | 4 | 0.029 | 0.14 |
| [5.6，5.8 | 2 | 0.014 | 0.07 |
| [5.8，6.0 | 1 | 0.007 | 0.04 |
| 合 计 | 140 | 1.000 |
（2）画频率分布直方图（略） …………………3分
（3）由频率分布表可知，红细胞数在正常值（4.0～5.5）的频率约为0．95，由此，估计成年男性的红细胞数在正常值（4.0～5.5）的概率为0．95．………………10分
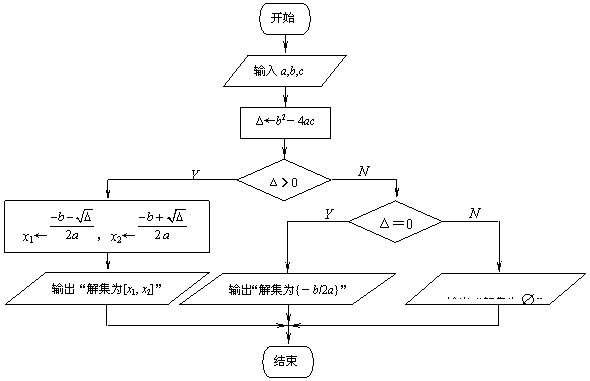20．算法流程图如下图所示（5分）：
伪代码是：（5分）
21．（1）能够判断出两人的观点都是错误的各得2分；
（2）说明理由正确（用列表法、树状图，或互斥事件的概率说明都可以，只要说明的正确即可）得6分．
22．伪代码为（5分）：
 |
流程图（略）（5分）．要注意
规范，要注意到是否严格按照
当型循环或直到型循环的流程
图要求来写，未按规范要求写
的，扣2分．
23．（1）散点图如图（4分）．
（2）证明过程（9分）．
具体参见教材的推导过程．
得处关于x,y的二元二次函数
展开式，得3分；
得到两个关于a,b的方程，再得4分；
得到结果，再得2分．（结果为
= 6.5x + 17.5）
直接利用公式得到结果的得2分．