高一数学下学期同步期中测试

　　

　

高一数学下学期同步期中测试

本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.

第Ⅰ卷（选择题，共50分）

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．

1．一个棱锥所有的棱长都相等，则该棱锥一定不是　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．三棱锥　　　　　　　B．四棱锥　　　　　　 C．五棱锥　　　　　　　 D．六棱锥

2．面积为Q的正方形，绕其一边旋转一周，则所得几何体的侧面积为　　　　　　　　　 （　　）

　　　 A．Q　　　　　 B．2Q　　　 　　　C． 3Q　 　　　　　 D． 4Q

3．已知高与底面的直径之比为2：1的圆柱内接于球，且圆柱的体积为500，则球的体积

　 为 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　 B． 　　 C． 　　D．

4．到空间四点距离相等的平面的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．4　　　　　　　　　　 B．7　　　　 　　　　 C．4或7　　 　　　　 D．7或无穷多

5．在阳光下一个大球放在水平面上, 球的影子伸到距球与地面接触点10米处, 同一时刻, 一根长1米一端接触地面且与地面垂直的竹竿的影子长为2米, 则该球的半径等于　　　　　　　　　　　（　　）

　　　 A．10（－2）米　　　　　　　　　　　　　　　 B．（6－）米　　 

　　　 C．（9－4）米　　 　　　　　　　　　　　　　 D．5 米

6．已知ABCD 是空间四边形，M 、N 分别是AB 、CD 的中点，且AC ＝4，BD ＝6，则　　 （　　）

A．1＜MN ＜5　　　 B．2＜MN ＜10 　　 C．1≤MN ≤5　　　 D．2＜MN ＜5

7．空间一个角的两边分别垂直于另一角的两边，则这两个角　　　　　　　　　　　　　　　　 （　　）

　　　 A．相等　　　　　　　B．互补　　　　　　　 C．相等或互补　　 D． 不确定

8．已知平面a ⊥平面b ，m 是a 内一条直线，n 是b 内一条直线，且m ⊥n ．那么，甲：m ⊥b ；乙：n ⊥a ；丙：m ⊥b 或n ⊥a ；丁：m ⊥b 且n ⊥a ．这四个结论中，不正确的三个是　　　　　　　　　　　　　 （　　）

A．甲、乙、丙 　　　 B．甲、乙、丁　　

C．甲、丙、丁　　 D．乙、丙、丁

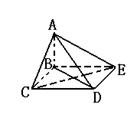
9．如图，A—BCDE 是一个四棱锥，AB ⊥平面BCDE ，且四边

　 形BCDE为矩形，则图中互相垂直的平面共有（　　）

　　　 A．4组　　B．5组　　C．6组　　 D．7组

10．棱台的两底面积分别为S_上、S_下、平行于底面的戴面把棱台的高自上而下分为两段之比

　　为m∶n则截面面S₀为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　 B．

　　　 C．()²　　　　　　　　　　　　　 D．()²

第Ⅱ卷（非选择题，共100分）

二、填空题：请把答案填在题中横线上（每小题6分，共24分）．

11．半径为a的球放在墙角，同时与两墙面和地面相切，那么球心到墙角顶点的距离为　　　　　　  ．

12．a 、b 是两个不同的平面，m 、n 是平面a 及b 之外的两条不同直线，给出四个论断：

（1）m ⊥n　　 （2）a ⊥b　　（3）n ⊥b　　 （4）m ⊥a　

　　　 以其中三个论断作为条件，余下一个论断作为结论，

　　　 写出你认为正确的一个命题___________．

13．如图，三棱柱ABC—A₁B₁C₁中，若E、F分

　　　 别为AB、AC 的中点，平面EB₁C₁将三棱柱

　　　 分成体积为V₁、V₂的两部分，那么V₁∶V₂= _____．

① ② ③ ⑤ ⑥ ④

① ⑤ ⑥ ④ ③ ②

④ ⑥ ① ⑤ ③ ②

④ ② ⑥ ③ ① ⑤

14．下图都是正方体的表面展开图，还原成正方体后，其中两个完全一样的是____________．

（1）　　　　　  （2）　　　　　　　  （3）　　　　　 （4）

三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．

15．（12分）如图，长方体ABCD－A₁B₁C₁D₁中被截去一部分，其中EF∥A₁D₁．剩下的几何体是什么？截取的几何体是什么？若FH∥EG，但FH<EG，截取的几何体是什么?

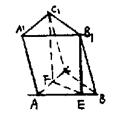
16．（12分）有一正三棱锥和一个正四棱锥，它们的所有棱长都相等，把正三棱锥和正四棱锥的一个全等的面重合．

　　　 ①说明组合体是什么样的几何体？

　　　 ②证明你的结论．

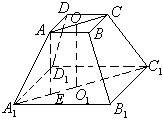
17．（12分）正四棱台的高，侧棱，对角线长分别为7cm，9cm，11cm，求它的侧面积．

18．（12分）三棱锥S-ABC的三条侧棱两两垂直，SA=5，SB=4，SC=3，D为AB中点，E为AC中点，求四棱锥S-BCED的体积．

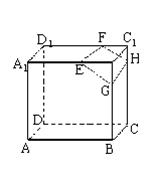
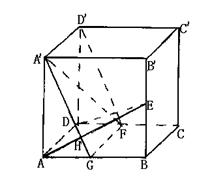
19．（14分）如图，在正方体

　 （1）证明：；

　 （2）求所成的角；

　 （3）证明：．

20．（14分）如图，△ABC 为正三角形，EC ⊥平面ABC ，BD ∥CE ，CE ＝CA ＝2 BD ，M 是EA 的中点，求证：

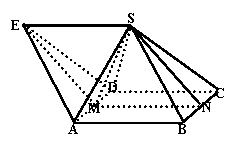
　 （1）DE ＝DA ；

　 （2）平面BDM ⊥平面ECA ；

　 （3）平面DEA ⊥平面ECA ．

高一新数学期中测试题参考答案

一、DBDDA　ADBCD．

二、11；12．①③④②；13．7∶5；14．②③；

三、15． 五棱柱，三棱柱，三棱台。

16．解：（1）是斜三棱柱。

（2）正三棱锥为S—AED，正四棱锥为S—ABCD，重

合的面为⊿ASD，如图示， 设AD，BC中点分别

为M、N，由AD⊥平面MNS知平面MES重合；

因为SE=AB=MN,EM=SN,∴MNSE为平行四边行。

∴ESMN，又ABMN，∴ESAB，∴ABSE

为平行四边形，同理，CDES为平行四边形。

∴面SBC∥面EAD，AB∥CD∥SE，且AB不垂

直平面SBC，∴组合体为斜三棱柱。

17．解：如图，在中过A作于E，

　　　 则AE=OO₁=7cm

18．解：

　　　

　　　

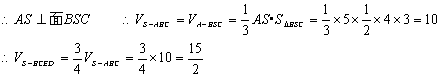
19． （1）

（2）

　　　

（3）

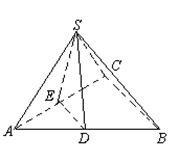
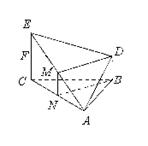
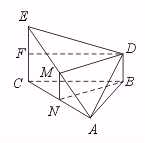20．证明：（1）如图，取EC 中点F ，连结DF ．

∵　EC ⊥平面ABC ，BD ∥CE ，得DB ⊥平面ABC ．

∴　DB ⊥AB ，EC ⊥BC ．

∵　BD ∥CE ，BD ＝CE ＝FC ，则四边形FCBD 是矩形，

DF ⊥EC ．　又BA ＝BC ＝DF ，

∴　Rt△DEF ≌Rt△ABD ，所以DE ＝DA ．

（2）取AC 中点N ，连结MN 、NB ，∵　M 是EA 的中点，

∴　MN EC ．由BD EC ，且BD ⊥平面ABC ，可得四边形

MNBD 是矩形，于是DM ⊥MN ．

∵　DE ＝DA ，M 是EA 的中点，　∴　DM ⊥EA ．又EA MN ＝M ，

∴　DM ⊥平面ECA ，而DM 平面BDM ，则平面ECA ⊥平面BDM ．

（3）∵　DM ⊥平面ECA ，DM 平面DEA ，∴　平面DEA ⊥平面ECA ．