新课标高一数学下学期同步期末测试
本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.
第Ⅰ卷（选择题，共50分）
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．
1．在斜二测画法中，与坐标轴不垂直的线段的长度在直观图中 （ ）
A．变大 B．变小 C．可能不变 D．一定改变
2．垂直于同一条直线的两条直线的位置关系是 （ ）
A．平行 B．相交
C．不在同一平面内 D． A、B、C均有可能
3．一个直角梯形的两底长分别为2和5，高为4，绕其较长的底旋转一周，所得的几何体的
表面积为 （ ）
A．
B．
C．
D．
4．直线y=kx+2与圆x2+y2+2x=0只在第二象限有公共点，则实数k的取值范围为 （ ）
A．[
，1] B．
，1） C．，+∞） D．（－∞，1）
5．已知球面上的四点P、A、B、C，PA、PB、PC的长分别为3、4、5，且这三条线段两两
垂直，则这个球的表面积为 （ ）
A．20
π B．25π C．50π D．200π
6．一个二面角的两个面与另一个二面角的两个面分别垂直, 则这两个二面角 （ ）
A．互补 B．互余 C．互补或互余 D．不确定
|
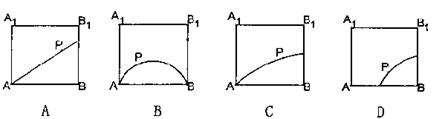
有一动点P，动点P到直线A1B1与直线BC的距离相等，
|
8．对于一个长方体，都存在一点：（1）这点到长方体各顶点距离相等（2）这点到长方体各条棱距离相等（3）这点到长方体各面距离相等。以上三个结论正确的是 （ ）
A．（1）（2） B．（2） C．（1） D．（1）（3）
9．直线
与直线
的交点的个数为 （ ）
A．0个 B．1个 C．2个 D．随a值变化而变化
|
支撑着一个平行四边形的太阳能电池板，可测得其中三
根立柱
、
、
的长度分别为
、
、
，
则立柱
的长度是（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题，共100分）
二、填空题：请把答案填在题中横线上（每小题6分，共24分）．
11．将边长为
的正方形钢板适当剪裁，再焊接成一个密闭的正四棱柱水箱，并要求这个水箱的全面积等于该正方形钢板的面积（要求剪裁的块数尽可能少，不计焊接缝的面积），则该水箱的容积为
．
12．过点P（3，6）且被圆
截得的弦长为8的直线方程为 ．
13．光线由点(－1，4)射出，遇直线2x＋3y－6=0被反射，已知反射光线过点(3 ，
)，反射光线所在直线方程__________________．
14．已知m、l是直线, 
是平面, 给出下列命题:
①若l垂直于
内的两条相交直线, 则
;
②若l平行于, 则l平行内所有直线;
③若
;
④若
;
⑤若
∥l．
其中正确的命题的序号是 (注: 把你认为正确的命题的序号都填上)．
三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．
15．（12分）已知两条直线l1 = x + my + 6 = 0, l2: (m－2)x + 3y + 2m = 0，问：当m为何值时, l1与l2(i)相交; (ii)平行; (iii)重合．
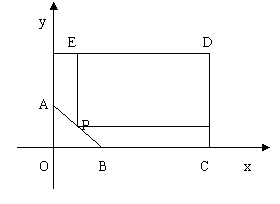
16．（12分）某房地产公司要在荒地ABCDE上划出一块长方形地面（不改变方位）建造一幢
八层楼的公寓，问如何设计才能使公寓占地面积最大？并求出最大面积（精确到1m2）.
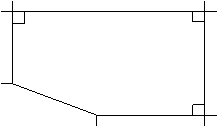E
100m
D
60m 80m
A
B 70m C
17．（12分）已知方程
的图形是圆.
（1）求t的取值范围；
（2）求其中面积最大的圆的方程．
18．（12分）自点P（－3，3）发出的光线
经过x轴反射，其反射光线所在直线正好与圆
相切，求入射光线所在直线的方程．
19．（14分）四棱锥P－ABCD中，底面ABCD是正方形，边长为a，PD=a，PA=PC=
，
（1）求证：PD⊥平面ABCD；
（2）求证，直线PB与AC垂直；
（3）求二面角A－PB－D的大小；
（4）在这个四棱锥中放入一个球，求球的最大半径；
（5）求四棱锥外接球的半径．
20．（14分）设M是圆
上动点，O是原点，N是射线OM上点，
若OM·ON＝120，求N点的轨迹方程．
高一新数学期末测试题参考答案
一、CDABC DCCDB
二、11．
；12．
和
；13．13x－26y＋85=0；14．①④；
三、 15．解： 若m = 0时，l1: x = －6，l2: 2x－3y = 0, 此时l1与l2相交；
若
，由
；
故i)当
, l1与l2相交；
ii)当m = －1时, 
, l1与l2平行；
(iii)当m = 3时
, l1与l2重合.
16．解：如图建立坐标系，在AB上任取一点P，分别向
CD、DE作垂线划得
一长方形土地，则直线AB的方程为
设
,则长方形的面积为
∴当X＝5时Smax≈6017
17．解：解：（1）方程即
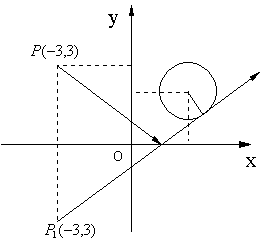
＞0 ∴
＜t＜1
（2） ∵
∴当t=
时，
，此时圆面积最大，所对应圆的方程是
18．解：设入射光线所在的直线方程为
，反射光线所在
直线的斜率为
，根据入射角等于反射角，得
，而点P（－3，3）关于x轴的对称点
（－3，－3），根据对称性，点在反射光线所在
直线上，故反射光线所在直线
的方程为：
即
，又此直线
与已知圆相切，所在圆心到直线
的距离等于半径
，因为圆心为（2，2），半径为1，所以
解得：
故入射光线所在的直线方程为：
或
即
19．解：⑴分析：要证PD⊥平面ABCD，只需证PD垂直于平面ABCD内的两条相交线，而所给已知
量都是数，故可考虑勾股定理的逆定理
⑴证明：∵PD=a，AD=a，PA=，∴PD2+DA2=PA2，同理∴∠PDA=90°.
即PD⊥DA，PD⊥DC，∵AO∩DC=D，∴PD⊥平面ABCD.
⑵分析：从图形的特殊性，应先考虑PB与AC是否垂直，若不垂直然后再转化
⑵解：连结BD，∵ABCD是正方形∴BD⊥AC ∵PD⊥平面ABCD∴PD⊥AC ∵PD∩BD=D
∴AC⊥平面PDB∵PBÌ平面PDB ∴AC⊥PB ∴PB与AC所成的角为90°
⑶分析：由于AC⊥平面PBD，所以用垂线法作出二面角的平面角
⑶解：设AC∩BD=0，过A作AE⊥PB于E，连接OE∵AO⊥平面PBD ∴OE⊥PB∴∠AEO为二面角 A－PB－D的平面角∵PD⊥平面ABCD，AD⊥AB∴PA⊥AB在Rt△PDB中，
，在Rt△PAB中，∵
∴
，
在Rt△AOE中，
，∴∠AEO=60°∴二面角A－PB－D的大小为60.
⑷分析：当所放的球与四棱锥各面都相切时球的半径最大，即球心到各个面的距离均相等，联想到用体积法求解
⑷解：设此球半径为R，最大的球应与四棱锥各个面都相切，设球心为S，连SA、SB、SC、SD、SP，则把此四棱锥分为五个棱锥，设它们的高均为R
∵ 
∴
∴
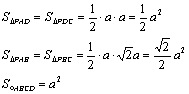
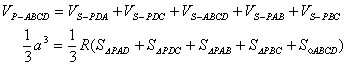
∴球的最大半径为（
）
⑸分析：四棱锥的外接球的球心到P、A、B、C、D五的距离均为半径，只要找出球心的位置即可，在Rt△PDB中，斜边PB的中点为F，则PF=FB=FD不要证明FA=FC=FP即可
⑸解：设PB的中点为F，∵在Rt△PDB中：FP=FB=FD
在Rt△PAB中：FA=FP=FB，在Rt△PBC中：FP=FB=FC
∴FP=FB=FA=FC=FD ∴F为四棱锥外接球的球心
则FP为外接球的半径 ∵FP=
∴
∴四棱锥外接球的半径为
评述：⑴本题主要考查棱锥的性质以及内切外接的相关知识点
⑵“内切”和“外接”等有关问题，首先要弄清几何体之间的相互关系，主要是指特殊的点、线、面之间关系，然后把相关的元素放到这些关系中解决问题，例如本例中球内切于四棱锥中时，球与四棱锥的五个面相切，即球心到五个面的距离相等
⑶求体积或运用体和解决问题时，经常使用等积变形，即把一个几何体割补成其它几个几何体的和或差
20．解：设M、N的坐标分别为
、
，
由题设
，得
（＊）
当M不在y轴上时，
，
，于是有
设＝
，代入（＊），化简得 
因
与
同号，于是
，
代入并化简，可得
当
时，
，点N
也在直线
上
所以，点N的轨迹方程为．