高一数学下学期同步测试1

高一数学下学期同步测试（1）—1.1空间几何体

本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.

第Ⅰ卷（选择题，共50分）

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．

1．直线绕一条与其有一个交点但不垂直的固定直线转动可以形成　　　　　　　　　　　　　（　　）

　　　 A．平面 　　　　　　　　 B．曲面　　　　　　　　　C．直线　　　　　　　　D．锥面

2．一个多边形沿不平行于矩形所在平面的方向平移一段距离可以形成　　　　　　　　　 （　　）

　　　 A．棱锥　　　　　　　　 B．棱柱　 　　　　　　　C．平面　 　　　　　　　D．长方体

3．有关平面的说法错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．平面一般用希腊字母α、β、γ…来命名，如平面α…

B．平面是处处平直的面

C．平面是有边界的面

D．平面是无限延展的

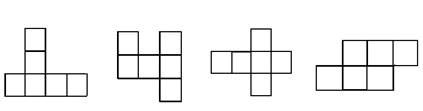
4．下面的图形可以构成正方体的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A　　　　　　　　　 B　　　　C　　　　　　　　　　D　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 5．圆锥的侧面展开图是直径为a的半圆面，那么此圆锥的轴截面是　　　　　　　　　　　 （　　）

　　　 A．等边三角形　　　　　　　　 　　　　　B．等腰直角三角形

　　　 C．顶角为30°的等腰三角形　　 　　　　 D．其他等腰三角形

6．A、B为球面上相异两点，则通过A、B两点可作球的大圆有　　　　　　　　　　　　　　　（　　）

　　　 A．一个 　　　　　　　　 B．无穷多个 　　　　　C．零个　　　　　　　　 D．一个或无穷多个

7．四棱锥的四个侧面中，直角三角最多可能有　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．1　　　　　　　　　　 B．2　　　 　　　　　　C．3　　 　　　　　　　 D．4

8．下列命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．由五个平面围成的多面体只能是四棱锥

　　　 B．棱锥的高线可能在几何体之外

　　　 C．仅有一组对面平行的六面体是棱台

　　　 D．有一个面是多边形，其余各面是三角形的几何体是棱锥

9．长方体三条棱长分别是AA′=1，AB=2，AD=4，则从A点出发，沿长方体的表面到

C′的最短矩离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．5　　　 　　　　　　B．7　　　　　　　　　C．　　 　　　　 D．

10．已知集合A={正方体}，B={长方体}，C={正四棱柱}，D={直四棱柱}，E={棱柱}，F={直平行六面体}，则　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　 B．

　　　 C．　　　　　　 D．它们之间不都存在包含关系

第Ⅱ卷（非选择题，共100分）

二、填空题：请把答案填在题中横线上（每小题6分，共24分）.

11．线段AB长为5cm，在水平面上向右平移4cm后记为CD，将CD沿铅垂线方向向下移动3cm后记为C′D′,再将C′D′沿水平方向向左移4cm记为A′B′，依次连结构成长方体ABCD—A′B′C′D′.

　　　①该长方体的高为　　　　 ；

　　　②平面A′B′C′D′与面CD D′C′间的距离为　　　　；

　　　③A到面BC C′B′的距离为　　　　 .

12．已知，ABCD为等腰梯形，两底边为AB,CD且AB>CD，绕AB所在的直线旋转一周所得的几何体中是由　　　　、　　　　 、　　　　的几何体构成的组合体.

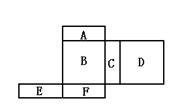
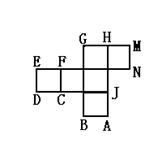
13．下面是一多面体的展开图，每个面内都给了字母，请根据要求回答问题：

①如果A在多面体的底面，那么哪一面会在上

面　　　　  ；

②如果面F在前面，从左边看是面B，那么哪一个

面会在上面　　　　  ；

③如果从左面看是面C，面D在后面，那么哪一

个面会在上面　　　　  .

14．长方体ABCD—A₁B₁C₁D₁中，AB=2，BC=3，

　　AA₁=5，则一只小虫从A点沿长方体的表面爬到C₁点的最短距离是 　　　　 ．

三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)

15．（12分）根据图中所给的图形制成几何体后，哪些点重合在一起．

16．（12分）若一个几何体有两个面平行，且其余各面均为梯形，则它一定是棱台，此命题是否正确，说明理由．

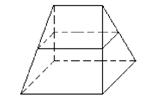
17．（12分）正四棱台上，下底面边长为a，b，侧棱长为c，求它的高和斜高．

18．（12分）把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1∶4，母线长10cm.求：圆锥的母长．

19．（14分）已知正三棱锥S-ABC的高SO=h,斜高SM=n,求经过SO的中点且平行于底面的截面△A₁B₁C₁的面积．

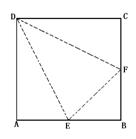
20．（14分）有在正方形ABCD中，E、F分别为AB、BC的中点，现在沿DE、DF及EF把△ADE、△CDF和△BEF折起，使A、B、C三点重合，重合后的点记为P.

　 问：

　　　①依据题意制作这个几何体；

②这个几何体有几个面构成，每个面的三角形为什么三角形；　　　　　　　　　　　　　　　　　　　　

　　　③若正方形边长为a，则每个面的三角形面积为多少．

参考答案（一）

一、DBCCA　 DDBAB

二、11．①3CM②4CM③5CM；　　12．圆锥、圆台、圆锥；　 13．①F②C③A；　 14．5．

三、15．解：J与N，A、M与D，H与E，G与F，B与C.

16．解：未必是棱台，因为它们的侧棱延长后不一定交于一点，如图，用一个平行于楔形底面的平面去截楔形，截得的几何体虽有两个面平行，其余各面是梯形，但它不是棱台，所以看一个几何体是否棱台，不仅要看是否有两个面平行，其余各面是否梯形，还要看其侧棱延长后是否交于一点.

　　　　小结：棱台的定义，除了用它作判定之外，至少还有三项用途：

　　　　①为保证侧棱延长后交于一点，可以先画棱锥再画棱台；

　　　　②如果解棱台问题遇到困难，可以将它还原为棱锥去看，因为它是由棱锥截来的；

　　　　③可以利用两底是相似多边形进行有关推算.

17．分析：棱台的有关计算都包含在三个直角梯形及两个直角三角形OBE和中，而直角梯形常需割成一个矩形和一个直角三角形对其进行求解，所以要熟悉两底面的外接圆半径（）内切圆半径（）的差，特别是正三、正四、正六棱台.

　　　　略解：

　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　  

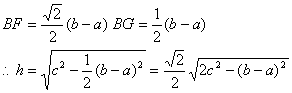
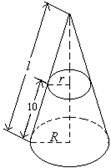18．解：设圆锥的母线长为，圆台上、下底半径为.

　　　　　　　　　　　　　　　　　　　　　　　　　　

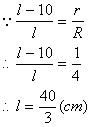
　　　　答：圆锥的母线长为cm.

19．解：设底面正三角形的边长为a，在RT△SOM中SO=h，SM=n，所以OM=，又MO=a，即a=，，截面面积为．

20．解：①略．

②这个几何体由四个面构成，即面DEF、面DFP、面DEP、面EFP.由平几知识可知DE=DF，∠DPE=∠EPF=∠DPF=90°，所以△DEF为等腰三角形，△DFP、△EFP、△DEP为直角三角形.

③由②可知，DE=DF=a,EF=a,所以，S_△DEF=a²。DP=2a，EP=FP=a，

　　　　所以S_△DPE= S_△DPF= a²，S_△EPF= a²．