高一数学下学期同步测试（10）—2.3圆的方程 YCY
YCY
本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.
第Ⅰ卷（选择题，共50分）
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．
1．直线x－y+3=0被圆（x+2）2+（y－2）2=2截得的弦长等于 （ ）
A．
B．
C．2 D．
2．圆x2＋y2＋2x＋6y＋9＝0与圆x2＋y2－6x＋2y＋1＝0的位置关系是 （ ）
A．相交 B．相外切 C．相离 D．相内切
3．过点P（2，1）作圆C：x2+y2－ax+2ay+2a+1=0的切线有两条，则a取值范围是（ ）
A．a＞－3 B．a＜－3
C．－3＜a＜－
D．－3＜a＜－或a＞2
4．设直线
与
轴的交点为P，点P把圆
的直径分为两段，
则其长度之比为 （ ）
A．
B．
C．
D．
5．圆
关于直线
对称的圆的方程是 （ ）
A．
B．
C． 
D．
6．如果实数
满足等式
，那么
的最大值是 （ ）
A．
B．
C．
D．
7．直线
与圆
交于E、F两点，则
（O为原点）
的面积为 （ ）
A．
B．
C．
D．
8．已知圆
的方程为
，且
在圆外，圆
的方程为
=
，则与圆一定 （ ）
A．相离 B．相切 C．同心圆 D．相交
9．两圆
，
的公切线有且仅有
（ ）
A．1条 B．2条 C．3条 D．4条
10．直线
与曲线
有且只有一个交点，则
的取值范围是 （ ）
A．
B．
且
C．
D．非A、B、C的结论
第Ⅱ卷（非选择题，共100分）
二、填空题：请把答案填在题中横线上（每小题6分，共24分）．
11．已知实数x，y满足关系：
，则
的最小值 ．
12．已知两圆
.求经过两圆交点的公共弦所在的直
线方程_______ ____．
13．过点M（0，4）、被圆
截得的线段长为
的直线方程为 _ _．
14．圆：
和：
的位置关系是_______ _____．
三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)
15．（12分）求过点P（6，－4）且被圆
截得长为
的弦所在的直线方程．
16．（12分）已知圆C:
及直线
.
（1）证明:不论
取什么实数,直线
与圆C恒相交；
（2）求直线与圆C所截得的弦长的最短长度及此时直线的方程．
17．（12分）一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮
船正西70 km处，受影响的范围是半径长30 km的圆形区域．已知港口位于台风正北
40 km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？
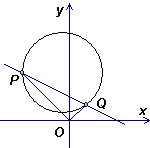
18．（12分）已知圆x2+y2+x－6y+m=0和直线x+2y－3=0交于P、Q两点，且以PQ为直径的
圆恰过坐标原点，求实数m的值．
19．（14分）已知圆
和直线
交于P、Q两点，且OP⊥OQ
（O为坐标原点），求该圆的圆心坐标及半径长．
20．（14分）求圆心在直线
上，且过两圆
，
交点的圆的方程．
参考答案（十）
一、DCDAA BCCBB．
二、11．
；12．
；13．x=0或15x＋8y－32=0；14．内切；
三、15．解：设弦所在的直线方程为
，即
①
|
|
则圆心（0，0）到此直线的距离为
．
因为圆的半弦长、半径、弦心距恰好构成Rt△，
所以
．
由此解得
或
．
代入①得切线方程
或
，即
或
．
16．解:(1)直线方程
,可以改写为
,所以直线必经过直线
的交点.由方程组
解得
即两直线的交点为A
又因为点
与圆心
的距离
,所以该点在
内,故不论取什么实数,直线
与圆C恒相交.
(2)连接
,过
作的垂线,此时的直线与圆相交于
、
.
为直线被圆所截得的最短弦长.此时,
.即最短弦长为
.
又直线的斜率
,所以直线的斜率为2.此时直线方程为:
17．解：我们以台风中心为原点O，东西方向为x轴，建立如图所示的直角坐标系．
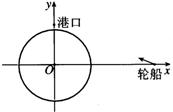这样，受台风影响的圆形区域所对应的圆的方程为
① 轮船航线所在直线l的方程为
，即
②
如果圆O与直线l有公共点，则轮船受影响，需要改变航向；如果
O与直线l无公共点，则轮船不受影响，无需改变航向．
由于圆心O（0，0）到直线l的距离
，
所以直线l与圆O无公共点．这说明轮船将不受台风影响，不用改变航向．
18．解：由
又OP⊥OQ， ∴x1x2+y1y2=0,而x1x2=9－6(y1+y2)+4y1y2= 
∴
解得m=3.
19．解：将
代入方程，
得
．
设P
，Q
，则
满足条件：
．
∵ OP⊥OQ,
∴
而
，
，
∴
．
∴
，此时Δ
，圆心坐标为（－
，3），半径
．
20．解法一：（利用圆心到两交点的距离相等求圆心）
将两圆的方程联立得方程组
，
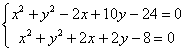解这个方程组求得两圆的交点坐标A（－4，0），B（0，2）．
因所求圆心在直线上，故设所求圆心坐标为
，则它到上面的两上交点
（－4，0）和（0，2）的距离相等，故有
，
即
，∴
，
，从而圆心坐标是（－3，3）．
又
， 故所求圆的方程为
．
解法二：（利用弦的垂直平分线过圆心求圆的方程）
同解法一求得两交点坐标A（－4，0），B（0，2），弦AB的中垂线为
，
它与直线交点（－3，3）就是圆心，又半径
，
故所求圆的方程为．
解法三：（用待定系数法求圆的方程）
同解法一求得两交点坐标为A（－4，0），B（0，2）．
设所求圆的方程为
，因两点在此圆上，且圆心在上，所以得方
程组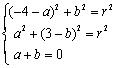 
，解之得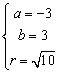
，
故所求圆的方程为．
解法四：（用“圆系”方法求圆的方程．过后想想为什么？）
设所求圆的方程为
，
即 
．
可知圆心坐标为
．
因圆心在直线上，所以
，解得
．
将代入所设方程并化简，求圆的方程
．