高一数学下学期同步测试（11）—2.4空间直角坐标系
YCY
本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.
第Ⅰ卷（选择题，共50分）
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）.
1．在空间直角坐标系中，已知点P（x，y，z），给出下列4条叙述：
①点P关于x轴的对称点的坐标是（x，－y，z）
②点P关于yOz平面的对称点的坐标是（x，－y，－z）
③点P关于y轴的对称点的坐标是（x，－y，z）
④点P关于原点的对称点的坐标是（－x，－y，－z）
其中正确的个数是 （ ）
A．3 B．2 C．1 D．0
2．若已知A（1，1，1），B（－3，－3，－3），则线段AB的长为 （ ）
A．4
B．2 C．4
D．3
3．已知A（1，2，3），B（3，3，m），C（0，－1，0），D（2，―1，―1），则 （ ）
A．
>
B．<
C．≤
D．≥
4．设A（3，3，1），B（1，0，5），C（0，1，0），AB的中点M，则
（ ）
A．
B．
C．
D．
|
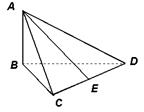
CD=2，点E为CD的中点，则AE的长为（ ）
A． B．
C．
D．
6．点B是点A（1，2，3）在坐标平面
内的射影，则OB等于 （ ）
A．
B．
C．
D．
7．已知ABCD为平行四边形，且A（4，1，3），B（2，－5，1），C（3，7，－5），则点D
的坐标为 （ ）
A．（
，4，－1） B．（2，3，1） C．（－3，1，5） D．（5，13，－3）
8．点
到坐标平面
的距离是 （ ）
A．
B．
C．
D．
9．已知点
，
， 
三点共线，那么
的值分别是 （ ）
A．
，4 B．1，8 C．
，－4 D．－1，－8
10．在空间直角坐标系中，一定点到三个坐标轴的距离都是1，则该点到原点的距离是（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题，共100分）
二、填空题：请把答案填在题中横线上（每小题6分，共24分）．
|
，
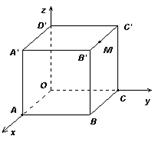
点M在
上，且
2
，以O
为坐标原点，建立如图空间直有坐标系，则点
M的坐标为 ．
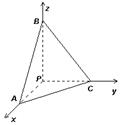
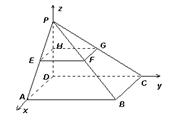
12．如右图，为一个正方体截下的一角P－ABC，
|
，
，
，建立如图坐标
系，求△ABC的重心G的坐标 _ _．
13．若O（0，0，0），P（x，y，z），且
，则
表示的图形是 _ _．
14．已知点A（－3，1，4），则点A关于原点的对称点
B的坐标为 ；AB的长为 ．
三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分)．
|
中，
，
，
，设E为
的中点，F为
的中点，在给定的空间直角坐标系D－xyz下，试写出A，B，C，D，
，
，
，
，E，F各点的坐标．
|
|
，
．将矩形ABCD沿对角线BD折起，使得面BCD⊥面ABD．现以D为原点，DB作为y轴的正方向，建立如图空间直角坐标系，此时点A恰好在xDy坐标平面内．试求A，C两点的坐标．
18．（12分）已知，，
，求证其为直角三角形．
|
的棱长为a，M为
的中点，点N在
上，且
，试求MN的长．
20．（14分）在空间直角坐标系中，已知A（3，0，1）和B（1，0，－3），试问
（1）在y轴上是否存在点M，满足
？
（2）在y轴上是否存在点M，使△MAB为等边三角形？若存在，试求出点M坐标．
参考答案（十一）
一、CADCB BDCCA
二、11．（2a，3a，3a）； 12．G（
） ； 13．以原点O为球心，以1为半径的球面；
14．（3，－1，－4）； 
；
三、
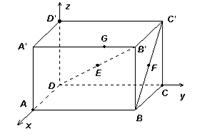
15．解：设原点为O，因为A，B，C，D这4个点都在坐标平面 xOy内，
它们的竖坐标都是0，而它们的横坐标和纵坐标可利用，写出，
所以 A（3，0，0），B（3，5，0），C（0，5，0），D（0，0，0）；
因为平面
与坐标平面xOy平行，且，所以A'，B'，，D'的竖坐标
都是3，而它们的横坐标和纵坐标分别与A，B，C，D的相同，所以（3，0，3），（3，5，3），（0，5，3），（0，0，3）；
由于E分别是中点，所以它在坐标平面xOy上的射影为DB的中点，从而E的横坐标和纵坐标分别是的
，同理E的竖坐标也是的竖坐标的，所以E（
）；
由F为中点可知，F在坐标平面xOy的射影为BC中点，横坐标和纵坐标分别为
和5，同理点F在z轴上的投影是AA'中点，故其竖坐标为，所以F（，5，）．
16．解: 由图形知，DA⊥DC，DC⊥DP，DP⊥DA，故以D为原点，建立如图空间坐标系D－xyz．
因为E，F，G，H分别为侧棱中点，由立体几何知识可知，平面EFGH与底面ABCD平行，
从而这4个点的竖坐标都为P的竖坐标的一半，也就是b，
由H为DP中点，得H（0，0，b）
E在底面面上的投影为AD中点，所以E的横坐标和纵坐标分别为a和0，所以E（a，0，b），
同理G（0，a，b）；
F在坐标平面xOz和yOz上的投影分别为点E和G，故F与E横坐标相同都是a，
与G的纵坐标也同为a，又F竖坐标为b，故F（a，a，b）．
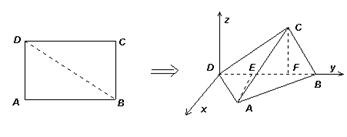
17．解： 由于面BCD⊥面ABD，从面BCD引棱DB的垂线CF即为面ABD的垂线，同理可得AE即为面BCD的垂线，故只需求得
的长度即可。
最后得A（
），C（0,
）
18．略解：利用两点间距离公式，
由
，
，
，从而
，结论得证.
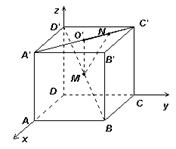
19．解：以D为原点，建立如图空间直角坐标系．因为正方体棱长为a，
所以B（a，a，0），A'（a，0，a），（0，a，a），（0，0，a）．
由于M为的中点，取
中点O'，所以M（
，，），O'（，，a）．
因为
，所以N为的四等分，从而N为
的中点，故N（
，
，a）．
根据空间两点距离公式，可得
．
20．解：（1）假设在在y轴上存在点M，满足．
因Ｍ在y轴上，可设M（0，y，0），由，可得
，
显然，此式对任意
恒成立．这就是说y轴上所有点都满足关系．
（2）假设在y轴上存在点M，使△MAB为等边三角形．
由（1）可知，y轴上任一点都有，所以只要
就可以使得△MAB是等边三角形．
因为
于是
，解得
故y轴上存在点M使△MAB等边，M坐标为（0，
，0），或（0，
，0）．