补充内容：空间向量及运算（三）

补充内容：空间向量及运算（三）

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 目标要点：

（1）进一步巩固空间向量的基本定理、空间向量数量积的意义及运算；

（2）初步掌握用向量处理空间的平行与垂直、求角与距离的基本方法。

二、　　　　　　 要点回顾：

1、共面向量定理：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

2、空间向量的基本定理：　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　 。

3、空间两向量的数量积是　　　　　　　　　  ，它的意义是　　　　　　　　　　　　　　　  。

4、=　　　　　　　　　　　  ；=　　　　　　　　  ；　　　　　　　 。

三、目标训练：

1、已知，若，则=　　　　　　　　  。

2、如果，则=　　　　　　　　　  。

3、如果，且，则　　　　　 ；　　　　　　 。

4、若是空间的一个基底，给出下列结论：（1）的最大值为；（2）的最小值为0；（3）的取值范围为，其中正确的结论为　　　 。

5、已知是不共面的三个向量，若它们的起点相同，且及的终点共面，则实数　。

6、已知线段AB、BD在平面内，∠ABD=120⁰，线段AC⊥，如果，则

　　　　　　　　　  。

7、已知空间四边形OABC中，M、N、P、Q分别为BC、AC、OA、OB的中点，若AB=OC，

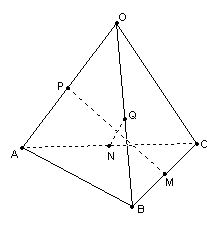求证：PM⊥QN。

8、用向量方法证明：若直线l//直线m，l⊥平面，则m⊥平面。

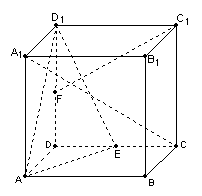
9、在正方体ABCD-A₁B₁C₁D₁中，E、F分别是棱CD、DD₁的中点，用向量方法：

（1）求证：A₁C//平面AED₁；（2）求异面直线AE与FC₁所成的角。

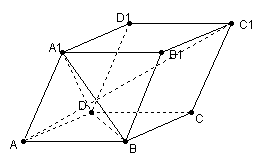
10、如图，已知平行六面体ABCD- A₁B₁C₁D₁的底面ABCD是菱形，且∠C₁CB=∠C₁CD=∠BDC；用向量方法：（1）求证：CC₁⊥BD；（2）当的值为多少时，能使A₁C⊥平面C₁BD？请给出证明。