补充内容：空间向量及运算（二）
班级 学号 姓名
一、 目标要点：
（1）掌握空间向量的基本定理，并能简单应用；（2）掌握空间向量数量积的意义及运算并能简单应用。
二、 要点回顾：
1、空间向量的基本定理是： 。
推论：设O、A、B、C是不共面的四点，则对空间任一点P，都存在 的有序实数组x,y,z使
=
。
2、空间任意三个不共面的向量都可构成空间的一个 ，这三个不共面的向量叫 。
3、
叫向量
与
的夹角，记作：
。
4、若
，则向量与互相垂直，记作：
。
5、已知空间两个向量与，则
叫做向量与的数量积，记作
，
即：=
。其几何意义是：
。
6、空间向量的数量积有下列性质：（1） （2） （3） 。
7、空间向量有如下运算律：（1） （2） （3） 。
三、 目标训练：
1、设命题P：、、
是三个非零向量；命题Q：
为空间的一个基底，则P是Q的（ ）
A、充分不必要条件 B、心要不充分条件 C、充要条件 D、既不充分也不必要条件
2、若是空间的一个基底，则下列各项中能构成基底的一组向量是
（ ）
A、
B、
C、
D、
3、已知向量、是平面
内的两个不相等的非零向量，非零向量在直线
上，则
且
是
的
（ ）
A、充分不必要条件 B、心要不充分条件 C、充要条件 D、既不充分也不必要条件
4、设A、B、C、D是空间不共面的四点，且满足
，
，
，则△BCD是
（ ）
A、钝角三角形 B、锐角三角形 C、直角三角形 D、不确定
5、给出下列命题：（1）空间任意三个不共面的向量都可以作为一个基底；（2）已知向量//，则、与任何向量都不能构成空间的一个基底；（3）A、B、M、N是空间四点，若
、
、
不能构成空间的一个基底，那么A、B、M、N四点共面；（4）若、、三向量两两不共线，则
的充要条件为
。其中真命题的是
。
6、已知线段AB、BD在平面内，∠ABD=120°，线段AC⊥，如果AB=
，BD=
，AC=
，则
为
。
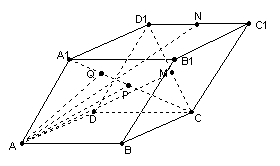
7、在平行六面体ABCD-A1B1C1D1中，
，
，
，P是CA1的中点，M是CD1的中点，N是C1D1的中点，点Q是CA1上的点，且CQ：QA1=4：1，用基底表示以下向量：
（1）
； （2）
； （3）
； （4）
。
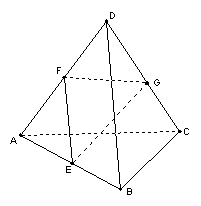8、已知空间四边形ABCD的每一条边和对角线的长都有等于a,，点E、F、G分别是AB、AD、DC的中点，求下列向量的数量积：（1）
； （2）
； （3）
；（4）
； （5）
； （6）
。
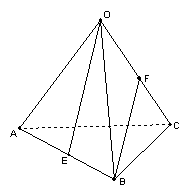9、点O是正三角形ABC平面外一点，若OA=OB=OC=AB=1，E、F分别是AB、OC的中点，试求
与
所成的角。