补充内容：空间向量的坐标运算（一）
班级 学号 姓名
一． 目标要点：
（1）掌握空间直角坐标系的概念；（2）掌握向量的坐标运算并能用于判定垂直和平行。
二．要点回顾：
1．如果空间的一个基底的三个基向量 ，且长为 ，则这个基底叫做 ，常用 表示。
2．在空间选定一点O和一个单位正交基底
，以O 为原点，分别以
的方向为正方向建立三条数轴：
。我们说建立了一个空间直角坐标系
，
点O叫做原点， 叫做坐标向量， 坐标平面。
3．给定一个空间直角坐标系和向量
，若存在数组
使
，则有序数组叫做
，记做
。
4．在空间直角坐标系
中，对空间任意一点A，对应一个向量
，若
，则称有序数组
是点A的
，记做
。
5．设
，
则：
； 
；
； 
；
； 
。
6．设A
，B
，则
。
三．目标训练：
1．已知点A，则点A 在坐标平面上的充要条件是
（ ）
A.
B.
C.
D
2.点P
在坐标平面
上的射影坐标为
, 在坐标平面
的射影坐标为
, 在坐标平面
上的射影坐标为
.
3. 点P关于原点成中心对称点的坐标为
, 关于平面上对称点的坐标为
.
4.已知向量
，
,
求:
(1) ,
(2) ；(3) 
；
(4) ;
(5)
; (6) 
;
(7)若
,求
.
 |
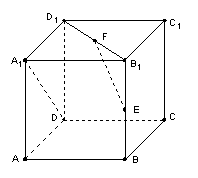5.在正方体
中,E,F分别是
的中点,求证:
(1)
;
(2)
6.已知四边形ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,试建立适当的坐标系.
(1)证明:MN⊥AB;
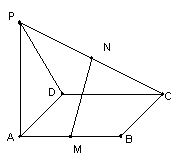(2)若平面PCD与平面ABCD成
的角,求证:MN⊥平面PCD.