两直线的位置关系及有关公式的应用练习
1、以下命题中的真命题是（ ）
A．平行直线的倾斜角相等 B．平行直线的斜率相等
C．互相垂直的两直线的倾斜角互补 D．互相垂直的两直线的斜率互为相反
2、两直线
和
的交点在
轴上，那么
的值是（ ）
A．
B．6 C．
D．不同于A、B、C的截
3、若直线
到直线
的角为
，到的角为
，则
的值为（ ）
A．
B．1 C．0
D．不能确定
4、点
在直线
上，O是原点，则OP的最小值是（ ）
A．
B．
C．
D．
5、过两直线
与
的交点，并且与第一条直线垂直的
直线方程是（ ）
A．
B．
C．
D．
6、如果直线
与直线
平行，那么系数
为（ ）
A．
B．
C．
D．
7、已知直线和的夹角的平分线为
，如果的方程为
，
那么的方程是（ ）
A．
B．
C．
D．
8、菱形ABCD的相对顶点
，则对角线
所在的直线方程为（ ）
A．
B．
C．
D．
9、已知直线：
，直线过点
，且到的角为
，
则的方程为（ ）
A．
B．
C．
D．
10、设直线：
与关于直线
对称，则直线的方程（ ）
A．
B．
C．
D．
11、已知点
和直线
：
，则过P与直线平行的直线方程是
，过点P与垂直的直线方程是
12、直线：
和直线：
相交于点
，且到
的角为
，则
13、直线
与直线
的夹角为
14、、直线
关于
轴对称的直线方程为
15、求垂直于直线
，且与两坐标轴构成周长为10的三角形的直线方程
16、一条光线从点
射出，与轴相交于点
，经过轴反射，求入射光线
和反射光线所在的直线的方程
17、求直线：
关于点
对称的直线的方程
18、求经过点
且到原点的距离等于1的直线方程
两直线的位置关系及有关公式的应用练习答案
1、A 2、C 3、C 4、B 5、B 6、B 7、A 8、A 9、D 10、B
11、
，
12、1，
13、
14、
15、解：由所求直线能与坐标轴围成三角形，则所求直线在坐标轴上的截距不为0，
故可设该直线在轴、轴上的截距分别为
，又垂直于直线，且与两坐标轴构成周长为10的三角形，故有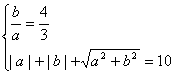
解得：
，
，所以所求直线方程为
或
16、解：光线从点射出，与轴相交于点，说明入射光线经过点，，所以反射光线所在直线方程为
，所以该直线与轴的夹角为，所以反射光线所在直线的倾斜角为
，且经过点，所以反射光线所在直线的方程为
17、解：设直线上任意一点，则关于点的对称点为
，又
在上，且有
，即
为的方程
18、解：（1）当过点的直线与轴垂直时，则点到原点的距离为1，所以
为所求直线方程
（2）当过点且与轴不垂直时，可设所求直线方程为
即：
原点到此直线的距离为1，
有
，解得
故所求的直线方程为
，即
综合（1）和（2）得所求直线方程为或
说明：解该类型题必须考虑直线的斜率是否存在