高一年级数学第二学期期中考试试卷
试卷页数:8页 考试时间:120分钟
一、选择题:(每小题3分,共36分)
1、若![]() 则
则![]() 的值是
的值是
A、 ![]() B、
B、 ![]() C、
C、 ![]() D、
D、 ![]()
2、点P在直线MN上,且![]() ,则点P分
,则点P分![]() 所成的比为
所成的比为
A ![]() B
B ![]() C
C
![]() D 2或
D 2或![]()
3、将向量![]() 按
按![]() 平移后的向量为
平移后的向量为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、下列函数中,周期为1的奇函数是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、若![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() ,则
,则![]() 等于
等于
A、![]() B、7
C、
B、7
C、![]() D、15
D、15
6、已知函数![]() 是常数,当
是常数,当![]() 时
时![]() 取最大值, 则θ的一个值是
取最大值, 则θ的一个值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、已知四边形OABC中,![]() 则
则![]()
A
![]() B
B ![]() C
C ![]() D
D ![]()
8、设O、A、B、C为平面上四个点,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,则
,则![]() 等于
等于
A.2![]() B.2
B.2![]() C.3
C.3![]() D.3
D.3![]()
9、已知钝角![]() 的终边经过点
的终边经过点![]() ,且
,且![]() ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、在![]() 中,
中,![]() ,则
,则![]() 的值为
的值为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、平面上A(-2,1),B(1,4),D(4,-3),C点满足![]()
![]() ,连DC并延长至E,使
,连DC并延长至E,使![]() =
=![]()
![]() ,则点E坐标为:
,则点E坐标为:
A、(-8,![]() ) B、(
) B、(![]() ) C、(0,1) D、(0,1)或(2,
) C、(0,1) D、(0,1)或(2,![]() )
)
12、△OAB中,![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,若
,若![]() =
=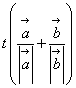 ,
,![]() ∈R,则点P一定在
∈R,则点P一定在
A、∠AOB平分线所在直线上 B、线段AB中垂线上
C、AB边所在直线上 D、AB边的中线上
二、填空题:(每小题3分,共12分)
13、已知点A(1, -2),若向量![]() 与
与![]() =(2,3)同向,
=(2,3)同向,![]() =2
=2![]() ,则点B的坐标为
,则点B的坐标为
14、函数![]() 的图象与
的图象与![]() 轴的各个交点中,离原点最近的一点的坐标为__________。
轴的各个交点中,离原点最近的一点的坐标为__________。
15、设![]() ,
,![]() ,
, ![]() 是任意的非零平面向量,且相互不共线,则:
是任意的非零平面向量,且相互不共线,则:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 不与
不与![]() 垂直
垂直
(4)![]() 中,
中,
真命题是________________________
16、定义运算![]() 为:
为: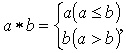 例如,
例如,![]() ,则函数f(x)=
,则函数f(x)=![]() 的值域为 。
的值域为 。
三、解答题:
17、(本题满分6分)
已知M、O、N三点共线,存在非零不共线向量![]() ,满足:
,满足:![]() ,
,![]() ,
,![]() ,求
,求![]() 的值。
的值。
18、(本题满分8分)
已知向量![]() .
.
(1)若点A、B、C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
19、(本题满分9分)
(1)已知![]() ,求
,求![]() 的值。(4分)
的值。(4分)
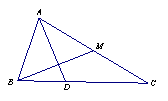 (2)如图:
(2)如图:![]() 中,
中,![]() ,D在线段BC上,且
,D在线段BC上,且![]() ,
,![]() 是中线,用向量证明
是中线,用向量证明![]() 。 (平面几何证明不得分)(5分)
。 (平面几何证明不得分)(5分)
20、(本小题满分9分)
已知:![]() 为常数)
为常数)
(1)若![]() ,求
,求![]() 的最小正周期;
的最小正周期;
(2)若![]() 在[
在[![]() 上的最大值与最小值之和为3,求
上的最大值与最小值之和为3,求![]() 的值;
的值;
(3)在(2)的条件下,函数![]() 的图象先按
的图象先按![]() 平移后再经过周期变换和振幅变换得到函数
平移后再经过周期变换和振幅变换得到函数![]() 的图象,求
的图象,求![]() .
.
21、(本小题满分8分)(普通班只做(1)(2);教改班只做(2)(3))
已知锐角△ABC中,![]() ,
,
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)设![]() ,求AB边上的高。
,求AB边上的高。
22、(本小题满分10分)(普通班做)
已知向量![]() 向量
向量![]() 与向量
与向量![]() 夹角为
夹角为![]() ,且
,且![]() .
.
(1)求向量![]() ;
;
(2)若向量![]() 与向量
与向量![]() =(1,0)的夹角为
=(1,0)的夹角为![]() ,其中A,C为△ABC的内角,且A,B,C依次成等差数列,试求
,其中A,C为△ABC的内角,且A,B,C依次成等差数列,试求![]() +
+![]() 的取值范围。
的取值范围。
22、(本小题满分10分)(教改班做)
已知向量![]() 向量
向量![]() 与向量
与向量![]() 夹角为
夹角为![]() ,且
,且![]() .
.
(1)若向量![]() 与向量
与向量![]() =(1,0)的夹角为
=(1,0)的夹角为![]() ,其中A,C为△ABC的内角,且A,B,C依次成等差数列,试求
,其中A,C为△ABC的内角,且A,B,C依次成等差数列,试求![]() +
+![]() 的取值范围。
的取值范围。
(2)若A、B、C为△ABC的内角,且A,B,C依次成等差数列,![]() ,设
,设![]() ,
,![]() 的最大值为
的最大值为![]() ,关于
,关于![]() 的方程
的方程![]() 在
在![]() 上有相异实根,求
上有相异实根,求![]() 的取值范围。
的取值范围。
 | |||
高一数学答卷纸
一、选择题:(每小题3分,共36分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题:(每小题3分,共12分)
13、____________________。 14、____________________。
15、____________________。 16、____________________。
三、解答题:
17、
18、
(1)
(2)
19、(1)
(2)
 |
20、
| 普通班 | 教改班 |
| ○ | ○ |
21、(请普通班的同学把表格中相应位置的“○”涂黑;教改班的同学把表格相应中位置的“○”涂黑)
![]() 22、
22、
| 普通班 | 教改班 |
| ○ | ○ |
(请普通班的同学把表格中相应位置的“○”涂黑;
教改班的同学把表格相应中位置的“○”涂黑)
 | |||
高一数学答案
一、选择题:(每小题3分,共36分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | C | A | D | B | D | C | C | D | A | B | A |
二、填空题:(每小题3分,共12分)
13、_______(5,
4)_______。 14、______![]() ________。
________。
15、_____(2)(4)_______。 16、______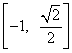 _______。
_______。
三、解答题:
17、设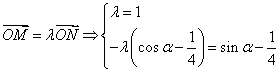
∴![]() , ∴
, ∴![]() 。
。
∵![]() , ∴
, ∴![]()
18、(1)若点A、B、C能构成三角形,则这三点不共线,
![]() 故知
故知![]()
∴实数![]() 时,满足的条件
时,满足的条件
(2) 若△ABC为直角三角形,且∠A为直角,则![]() ,
,
![]() 解得
解得![]()
19、(1) ∵![]() ,∴
,∴![]()
∴![]() =
=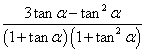 =
=![]()
 (2):
(2):![]() ,
,![]() ,
,
∴![]()
∴![]()
20、![]()
(1)最小正周期![]()
(2)![]()
![]()
|
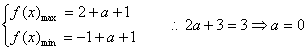
![]() (3)
(3)![]()
![]()
![]()
| 普通班 | 教改班 |
| ○ | ○ |
21、(请普通班的同学把表格中相应位置的“○”涂黑;教改班的同学把表格相应中位置的“○”涂黑)
(1)∵![]() ,∴
,∴![]() ,
,
∴![]()
∴![]()
(2)把![]() 展开即可得证。
展开即可得证。
(3)∵![]() , ∴
, ∴![]()
即![]() , 又
, 又![]() ,
,
∴![]() ,解得:
,解得:![]() ,舍负值,
,舍负值,
∴![]() ,∴
,∴![]()
设AB边上的高为CD,则![]() ,
,
由![]() 得:
得:![]()
| 普通班 | 教改班 |
| ○ | ○ |
22、(请普通班的同学把表格中相应位置的“○”涂黑;
教改班的同学把表格相应中位置的“○”涂黑)
(1)设![]() ,有
,有![]() ①
①
由![]() 夹角为
夹角为![]() ,有
,有![]() .
.
∴![]() ②
②
由①②解得![]() ∴即
∴即![]() 或
或![]()
(2)由![]() 垂直知
垂直知![]()
由2B=A+C 知![]()
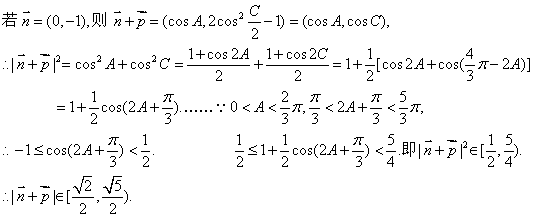 (3)
(3)![]() , 设
, 设![]() ,则
,则![]() ,其中
,其中![]()
![]() =
=![]()
∴![]() ∴
∴![]()
∵![]() ,∴
,∴![]()
∴方程![]() ,即为
,即为![]()
∵该方程在![]() 上有相异实根,∴
上有相异实根,∴![]() 。
。