§4.9 函数
的图象（三）
班级 学号 姓名
一、课堂目标： 由已知函数的图象写
型的解析式，及正弦型函数的综合应用。
二、 要点回顾：
1、
在一个周期内的五个关键点。如
的五个关键点分别是 、
、 、 、 。
2、
型函数的最大值是
，最小值是 ，周期是 ，
单调递增区间是 ，对称轴是 。
三、 目标训练：
1、1、函数在同一周期内，当
时，
当
时，
则此函数的解析式为（
）
A、
B、
C、
D、
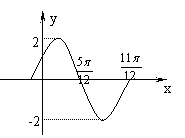2、已知右图是
的图象，则（
）
A、
B、
C、
D、
3、函数
的图象关于原点中心对称的充要条件是（ ）
A、
B、
C、
D、
4、函数
的图象向右平移
个单位，再将横坐标缩短到原来的
倍，则所得到的函数的解析式是
。
5、函数
的最小值为
，周期为
，且它的图象过点
，则这个函数的解析式是
。
6、若将函数
图象上每一点的纵坐标保持不变，将横坐标伸长到原来的2倍，然后再将图象向左平移
个单位，得到的图象与
的图象重合，则
。
7、关于函数
有下列命题：①由
可得
必是
的整数倍；②
的表达式可改写成
；③的图象关于直线
对称；④的图象关于点
对称 。其中正确命题的序号为
。
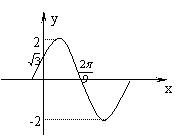
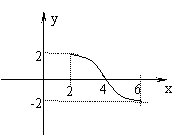8、已知函数
的一段图象（如下图）：
（1） （2）
则（1）
（2）
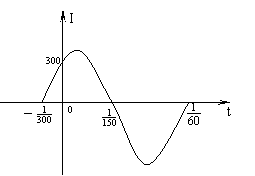9、已知如图表示电流I与时间t的关系式
在一个周期内的图象，
（1）根据图象写出的解析式；
（2）为了使中t 在任意一段
的时间内，电流I能同时取得最大值与最小值，求正整数
的最小值是多少？
10、已知函数
。
（1） 求函数
的周期； （2）求函数的单调递减区间；
（3）当函数取得最大时，求自变量
的集合；
（4）该函数的图象可由
通过怎样的平移和伸缩变换得到？