§4.9 函数
的图象（四）
班级 学号 姓名
一、课堂目标： 
的图象的综合应用。
二、 要点回顾：
1、要得到
的图象，只须把
的图象向
平移
个单位。
2、函数
的图象的对称轴是
。
3、把函数
的图象向右平移
个单位，再将图上各点的横坐标压缩到原来的
，所得图象的解析式是
。
4、已知函数
的单调递减区间是
。
三、 目标训练：
1、把函数
的图象适当变换就可以得到
的图象，这种变换可以是（ ）
A、沿
轴方向向右平移
个单位
B、沿轴方向向左平移个单位
C、沿轴方向向右平移
个单位
D、沿轴方向向左平移个单位
2、将
的图象向右平移个单位后，再关于轴作对称图形而得到
的图象，则
是（ ）
A、
B、
C、
D、
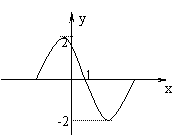3、右图是周期为
的三角函数
的图象，那么可以写成（ ）
A、
B、
C、
D、
4、（1）若
的图象关于
对称，求最大的负数
的值。
（2）若
的图象关于
对称，求a的值。
5、是否存在实数
，使得函数
是奇函数，且在
上是增函数？若存在，请写出任意两个值；若不存在，请说明理由。
6、一根长为
的线，一端固定，另一端悬挂一个小球。小球摆动时，离开平衡位置的位移
（单位：
）与时间
（单位：）的函数关系是
（1） 求小球摆动的周期；
（2）
已知
，要使小球摆动的周期是
，线的长度应当是多少（精确到
，
取
）？
7、受日月引力，海水会发生涨落，这种现象叫潮汐。在通常情况下，船在涨潮时驶进航道，靠近船坞；卸货后落潮时返回海洋。某港口水的深度
（米）是时间
的函数，记作
，下面是该港口在某季节每天水深的数据：
| t（时） | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| Y（米） | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
经长期观察，曲线可以近似地看作函数
的图象。
（1）
根据以上数据，求出函数的近似表达式。
（2） 一般情况下，船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的（船舶停靠时，船底只需不碰海底海底即可），某船吃水深度（船底离水面的距离）为6.5米。如果该船想在同一天内安全出港，问它至多能在港内停留多长时间（忽略进出港所需的时间）？