直线与平面复习（三）—平面与平面

直线与平面复习（三）—平面与平面

班级　　　　 学号　　　　　  姓名　　　　　  

一、选择题：

1．下列命题：① 若直线a //平面α，平面α⊥平面β，则a⊥β; ② 平面α⊥平面β，平面β⊥平面γ，则α⊥γ；③ 直线a⊥平面α，平面α⊥平面β，则a//β； ④ 平面α//平面β，直线a平面α，则a//β．其中正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　  （　　　　）

 （A）1　　　　（B）2　　　　 （C）3 　　　 （D）4

2．二面角α－AB－β的平面角为锐角，C是α内的一点（它不在棱AB上），点D是C在平面β内的射影，点E是AB上满足∠CEB为锐角的任意一点，那么（　　　 ）

（A）∠CEB>∠DEB　（B）∠CEB<∠DEB　（C）∠CEB=∠DEB　（D）无法确定

3．若有平面与，且，则下列命题中的假命题为　　　　  （　　　　）

（A）过点且垂直于的直线平行于（B）过点且垂直于的平面垂直于

（C）过点且垂直于的直线在内　（D）过点且垂直于的直线在内

4．已知l⊥α，mβ，则下面四个命题：　①α∥β则l⊥m　　②α⊥β则l∥m　 ③l∥m则α⊥β

　 ④l⊥m则α∥β其中正确的是　　　　　　　　　　　　　　　　　　　　　　　　（　　　　）

（A）①②　　　　（B）③④　　　 （C）②④　　　　（D）①③

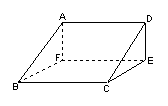5．已知：矩形ADEF⊥矩形BCEF，记∠DBE＝α，∠DCE＝β，∠BDC＝θ，则　　　（　　 　）

（A）sinα＝sinβcosθ　　　（B）sinβ＝sinαcosθ

（C）cosα＝cosβcosθ　　 （D）cosβ＝cosαcosθ

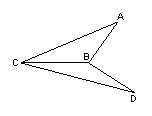
6． △ABC和△DBC所在的平面互相垂直，AB＝BC＝BD，

∠ABC＝∠DBC＝120°，则二面角A－BD－C的正切值为　　　　　　　　　　  　 （　　 　）　　　　　　　　　　　　　　　　　　　　　　　

（A）2　　　 （B）－2　　　 （C）　　　　 （D）－

7．二面角α―l―β的平面角是120°，在面α内，AB⊥l于B，AB＝2，在面β内，CD⊥l于D，CD＝3，BD＝1，M是棱l上的一个动点，则AM＋CM的最小值是　　　　　　　　　　　　 （　　　　）

（A）2　　　　（B）2　　　 （C）　　　 （D）2

8．在矩形ABCD中，AB=a，AD=2b，a<b，E、F分别是AD、BC的中点，以EF为折痕把四边形EFCD折起，当时，二面角C—EF—B的平面角的余弦值等于　　　　　　　  （　　 　 ）

　　A．0　　　　　B．　　 C．　　　D．

二、填空题：

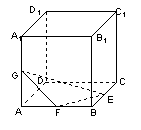
9．如图所示，E、F、G是正方体ABCD－A₁B₁C₁D₁相应棱的中点，则（1）面EFG与面ABCD所成的角为　　　　  ；（2）面EFG与面ADD₁A₁所成的角为　　　　　　 ．

10．在直二面角α－l－β中，A∈α，B∈β，AB与α所成的角为，AB与β所成的角为，AB与l所成的角为，则＝　　　　　　 ．

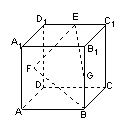
11．如图，在棱长为1的正方体ABCD－A₁B₁C₁D₁中，G、E分别为BB₁、C₁D₁的中点，点F是正方形ADD₁A₁的中心，则四边形BGEF在正方体六个面内的射影图形的面积的最大值为　　　　　　 ．

12．在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB²+AC²=BC².”拓展到空间，类比平面几何的勾股定理，研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则　　　　　　　　　　　　　　   ”．

三、解答题：

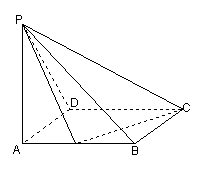13．如图，P是边长为a的正方形ABCD外一点，PA⊥平面ABCD，E为AB的中点，且PA＝AB．

（1）求证：平面PCE ⊥平面PCD；（2）求点D到平面PCE的距离．

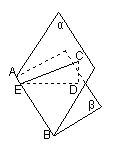
14． 已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，

∠ADB=60°，E、F分别是AC、AD上的动点，且

　 （Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；

　 （Ⅱ）当λ为何值时，平面BEF⊥平面ACD？