直线与平面复习（二）—直线与平面

直线与平面复习（二）—直线与平面

班级　　　　 学号　　　　　  姓名　　　　　  

一、选择题：

1、下列命题：① 一条直线在平面内 的射影是一条直线；② 在平面内射影是直线的图形一定是直线；③ 在同一平面内的射影长相等，则斜线长相等；④ 两斜线与平面所成的角相等，则这两斜线互相平行。其中真命题的个数是　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　（　　　 ）

　 （A）0个　　　　（B）1个　　　（C）2个　　　　（D）3个

2、若a, b表示两条直线，α表示平面，下面命题中正确的是　　　　　　　　　　　　　　  （　　　）

　（A）若a⊥α, a⊥b，则b//α 　　 （B）若a//α, a⊥b，则b⊥α

　（C）若a⊥α,bα，则a⊥b　　 （D）若a//α, b//α，则a//b

3、已知直线a平行于平面α，且它们的距离为d，则到直线a与到平面α的距离都等于d的点的集合是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 　）

　（A）空集　　　 （B）二条平行直线 　　 （C）一条直线　　 （D）一个平面

4、给出的是长方体形木料，想象沿图中平面所示位置截长方体，若那么截面图形是下面四个图形中的（　 ）

　 　　　　　 A　 　　　B　　　　C　　　　D

5、如果直角三角形的斜边与平面平行，两条直角边所在直线与平面所成的角分别为，则（　　）

（A） （B） （C） （D）

6、如果α∥β，AB和AC是夹在平面α与β之间的两条线段，AB⊥AC，且AB＝2，直线AB与平面α所成的角为30°，那么线段AC的长的取值范围是　　　　　　　　　　　　　　　　　　　 （　　　）

（A）　 （B）　　（C）　　  （D）

7、长方体ABCD-A₁B₁C₁D₁中，对角线AC₁与面ABCD、面BCC₁B₁所成的角分别为α、β，面对角线BC₁与面ABCD所成的角为γ，则有　　　　 　　　　　　　　　　　　　　　　(　　　 )

(A)sinα=sinβsinγ　（B）cosα=sinβcosγ　（C）cosα=cosβcosγ　（ D）sinα=cosβsinγ

8、已知四棱锥底面四边形中顺次三个内角的大小之比为2：3：4，此棱锥的侧棱与底面所成的角相等，则底面四边形的最小角是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）

　　A．　　　　　　　　 B．60　　　　　　　　　　C．　　　　　　　　 D．无法确定的

二、填空题：

9、正方形ABCD在平面α的同侧，若A、B、C三点到α的距离分别为2，3，4，则BD所在直线与平面α的位置关系是　　　　　　　  ．

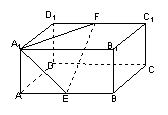
10、在长方体ABCD－A₁B₁C₁D₁中，AB＝，AA₁＝1，AD＝，E、F分别是AB、C₁D₁的中点，则直线A₁B₁与平面A₁EF所成的角为　　　　　  。

11、设正方体，恰好到其中5个面所在平面的距离都相等的点共有　　　　  个，若平面M与各条棱所成的角都等于，则　　　　 ．

12、在体对角线长为l的长方体中，体对角线在相邻三个面内的射影长的和的最大值等于___　　　 ．

三、解答题：

13、在立体图形P－ABCD中，底面ABCD是一个直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝a，

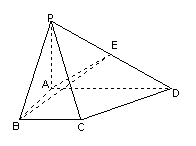AD＝2a，且PA⊥底面ABCD，PD与底面成30°角．

（1）若BE⊥PD于E，求证：AE⊥PD；

（2）求异面直线AE与CD所成的角．

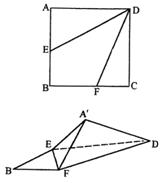
14、正方形ABCD中，AB=2，E、F分别是边AB及BC的中点，将△AED及△DCF折起（如图），使A、C点重合于点。　 （1）证明D⊥EF；　（2）求三棱锥—EFD的体积；

 （3）求D与平面DEF所成角的正切值.

15、如图，在直三棱柱ABC-A₁B₁C₁中，底面是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的重心G。求：（1）A₁B与平面ABD所成角的大小；（2）点A₁到平面AED的距离。（03高考题）