补充内容：空间向量及运算（一）

补充内容：空间向量及运算（一）

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 目标要点：

（1）了解空间向量的概念，掌握空间向量的加减与数乘运算。

（2）掌握共线与共面向量定理，并能进行简单的应用。

二、　　　　　　 要点回顾：

1、在空间，我们把具有　　　　　　　　　　　　  的量叫向量。

2、空间向量用有向线段表示时，　　　　　　　　　　　　　　  的有向线段表示同一向量或相等的向量。

3、如果表示空间向量的有向线段所在的直线　 　　　　　　　　　，则这些向量叫共线向量或平行向量。

4、共线向量定理：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

　 推论：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

　 空间直线的向量参数表示式是　　　　　　　　　　　　　 或　 　　　　　　　　　　　 。

5、共面向量定理：如果两个向量不共线，则向量与向量共面的充要条件是　　　　　　　　　 

　　　　　　　　　　　　　 。

推论：空间一点P位于平面MAB内的充分必要条件是存在实数对x,y使　　　　　　　　　　 ，或对空间任一点O，有　　　　　　　　　　　　　　　　  。

三、　　　　　　 目标训练：

1、下列四个等式：①；②；③；④，其中正确的是　　　　　　　 。

2、在下列命题中：①若与共线，则存在唯一的实数，使；②若存在唯一实数使，则与共线；③与任一向量都共线的向量是不存在的。其中正确的命题有　　　　　　　　　　　 。

3、在长方体ABCD-A₁B₁C₁D₁中，下列各式运算结果为的是　　　　　　　　　　　  。

①；②；③；④

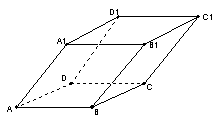4、在平行六面体ABCD-A₁B₁C₁D₁中，（1）所有与相等的向量是　　　　　　　　　　　　 ；（2）向量是否共面？　　　　　　  ；（3）设，E、F分别是AD1，BD的中点，则　　　　　　　　　　 。

5、在以下命题中：①若与是共线向量，则与所在直线平行；②若与所在直线是异面直线，则与一定不共面；③若三向量两两共面，则三向量一定也共面；④若三向量共面，则由所在直线所确定的平面与由所在直线所确定的平面一定平行。其中是假命题的为　　　　　　　  。

6、对于不共面的向量，如果，则

　　　　 ；　　　　　 ；　　　　　　  。

7、已知A、B、C三点不共线，对于平面ABC外一点O，确定在下列条件下，点M是否与A、B、C共面。

（1） 　　　　　　 ； （2）　　　　　　　　　。

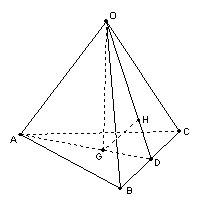8、空间四边形OABC中，G、H分别是ABC、OBC的重心，设，，，试用向量表示向量和。

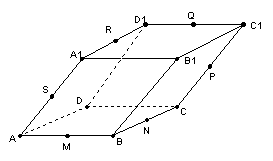9、在平行六面体ABCD-A₁B₁C₁D₁中，M、N、P、Q、R、S分别是AB、BC、CC₁、C₁D₁、D₁A₁、A₁A的中点，试证：。

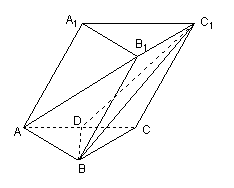
10*、如图，三棱柱ABC-A₁B₁C₁中，底面△ABC是正三角形，D为AC中点，求证：AB₁//平面C₁BD。