点、线、面之间的位置关系及线面平行应用练习
1、
平面
，点
，且
，又
，过
A、B、C三点确定的平面记作
，则
是（ ）
A．直线AC B．直线BC C．直线CR D．以上都不对
2、空间不共线的四点，可以确定平面的个数是（ ）
A．0 B．1 C．1或4 D．无法确定
3、在三角形、四边形、梯形和圆中，一定是平面图形的有 个
4、正方体
中，P、Q分别为
的中点，则四边形
是（ ）
A．正方形 B．菱形 C．矩形 D．空间四边形
5、在空间四边形
中，点E、F、G、H分别为AB、BC、CD、DA的中点，若AC=BD，
且
，则四边形EFGH为
6、下列命题正确的是（ ）
A．
若
，则直线
为异面直线
B．
若
，则直线为异面直线
C．
若
，则直线为异面直线
D．不同在任何一个平面内的两条直线叫异面直线
7、在空间中：①若四点不共面，则这四点中任何三点都不共线；②若两条直线没有
公共点，则这两条直线是异面直线，以上两个命题中为真命题的是
8、过直线L外两点作与直线L平行的平面，可以作（ ）
A．1个 B．1个或无数个 C．0个或无数个 D．0个、1个或无数个
9、
，且
与平面
相交，那么直线
与平面的位置关系是（ ）
A．必相交 B．有可能平行 C．相交或平行 D．相交或在平面内
10、直线与平面平行的条件是这条直线与平面内的（ ）
A．一条直线不相交 B．两条直线不相交
C．任意一条直线不相交 D．无数条直线不相交
11、如果两直线，且
平面，则与平面的位置关系是（ ）
A．相交 B．
C．
D．或
12、已知直线与直线垂直，平行于平面，则与平面的位置关系是（ ）
A．
B．
C．与平面相交 D．以上都有可能
13、若直线与直线是异面直线，且平面，则与平面的位置关系是（ ）
A．
B．与平面相交 C．
D．不能确定
14、已知平面，直线，则直线与直线的关系是（ ）
A．相交 B．平行 C．异面 D．平行或异面
15、平面
平面
，平面
平面
，平面
平面
，若，
则
与的位置关系是（ ）
A．与异面
B．与相交
C．至少与中的一条相交 D．与都平行
16、是异面直线，则过且与平行的平面有
个
17、正方体的棱长为，求异面直线
和
所成的角的余弦值
18、已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点，求证：
AM
面EFG
19、在正方体中，E为
的中点，求证：∥面AEC
20、在正方体中，E、F分别为BC、
的中点，
求证：EF//平面
21、已知在正方体中，E、F分别是的中点，求证：
平面
平面
22、过正方体的棱
作一平面交平面
于
，
求证：//
23、如图，四边形ABCD是矩形，
面ABCD，过BC作平面BCFE交AP于E，
|
|
|
|
|
|
|
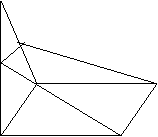交DP于F，求证：四边形BCFE是梯形
点、线、面之间的位置关系及线面平行应用练习答案
1、C 2、C 3、3
4、B 5、正方形 6、D 7、① 8、D（提示：当
时，就为
0个） 9、A 10、C 11、D 12、D 13、D 14、D 15、D 16、1 17、
18、提示：连结MD交GF于H，则点H为MD的中点
19、提示：连接
交
于点O，连接EO，则EO//，又
面
，
故//面
20、提示：取
的中点为
，连接
，则
且
，则
四边形
是平行四边形，故
21、提示：
，取的中点H，连接EH，
，有
所以四边形
是平行四边形，所以
，又
，
所以
22、分析：因为//
面，所以//面
23、分析：因为
，所以BC//面ADP，所以BC//EF，所以EF//AD，但EF的长度
小于
的长度，而
，所以EF的长度小于BC的长度